逻辑函数的图形化简法

一、最小项
1．最小项的特点（以三变量A，B，C为例）每项都只有三个因子（A，B，C）；每个变量都是它的一个因子；每一变量或以原变量(A，B，C)形式出现，或以非变量(A非，B非，C非)形式出现；每个乘积项的组合仅出现一次，且取值为
1；最小项可以编码。
2．最小项表达式及书写形式：最小项表达式是由若干个最小项相加的与—或表达式。任何一个逻辑表达式都可以化成最小项表达式。
2.一个逻辑函数，如果有n个变量，则有2ⁿ个最小项。
最小项的基本性质：

• a．只有一组取值使之为“1”
• b．任二最小项乘积与“0”
• c．所的最小项之和为“1”

例：3变量A，B，C，有2³＝8个最小项，其形式为：


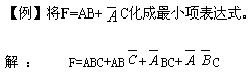
二、卡诺图（Karnaugh Map）

1．卡诺图画法：

三变量卡诺图: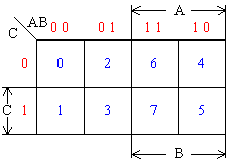

说明:三变量卡诺图由8个最小项m₀—m₇组成，每个最小项占一个方格；
AB组合中左数位代表A变量，右数位代表B变量。沿横向从一个方格进行到下一个方格时，两个数位只变化一个； 原变量与非变量各占4格。
四变量卡诺图: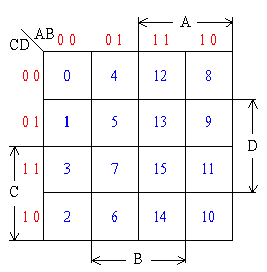

说明:
四变量卡诺图由16个最小项m₀—m₁₅组成，每个最小项占一个方格；纵向方向因有两个变量CD，增加了8个方格，CD变化规律同AB；原变量与非变量各占8格。
2．相邻的概念

二小格相邻组合:
例如:卡诺图中，有F（A，B，C，D）=∑m(2，3，8，10，12)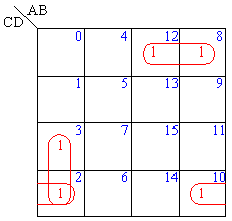

（m₈、m₁₂）、（m₂、m₃）几何相邻，（m₂、m₁₀）逻辑相邻
四小格相邻组合：四小格相邻时，4个最小项可合并成1项，且可消去两个变量。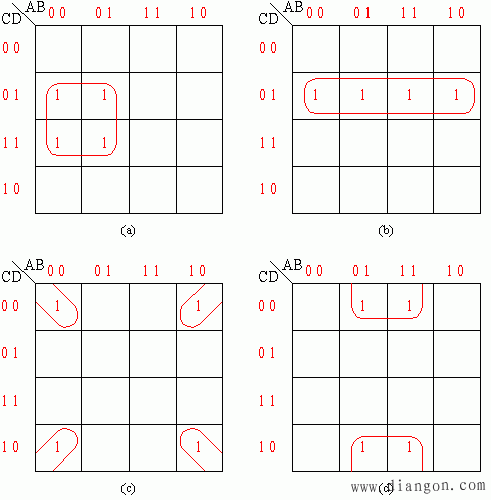

八方格相邻组合：
八方格相邻时，8个最小项可合并成1项，且可消去三个变量。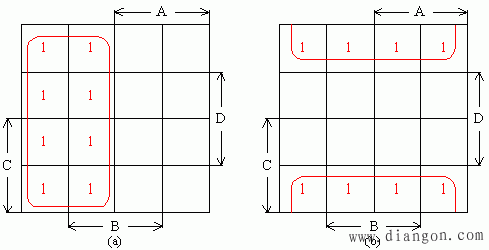

三、用卡诺图简化逻辑函数

1． 用卡诺图化简逻辑函数基本步骤：

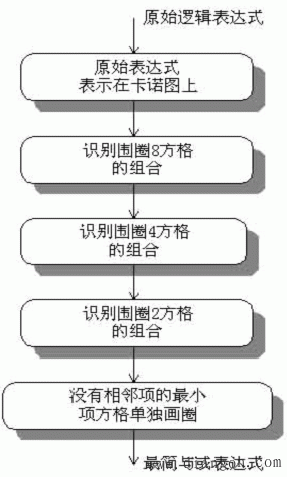
2．几个注意点：

1. 必须使每个方格(最小项)至少被包含一次；
2. 使每个组合包含尽可能多的方格；
3. 所有的方格包含在尽可能少的不同组合中。
4. 未用最小项表示的逻辑函数的简化：逻辑函数未用(最小项)表示照样可以化简。（http://www.ippipp.com/版权所有 )如果F采用与—或表达式，在填入卡诺图过程中先把函数展开成标准与--或式，再填入卡诺图中进行化简。

3． 具有约束项的逻辑函数的化简

任意项又叫无关项，是一种最小项，其值可以取0或1。利用任意项这一特点，可以使函数简化。 任意项用“×”（或“d”）表示，利用无关项化简原则：① 无关项即可看作“1”也可看作“0”。②卡诺图中，圈组内的“×”视为“1”，圈组外的视为“0”。