公式化简法的原理就是反复使用逻辑代数的基本公式和常用公式消去函数式中多余的乘积项和多余的因式，以求得函数式的最简形式。
公式化简法没有固定的步骤。现将经常使用的方法归纳如下：
一、并项法
二、吸收法
利用公式A+AB=A，吸收掉（即除去）多余的项。A和B同样也可以是任何一个复杂的逻辑式。
【例】试用吸收法化简下列逻辑函数：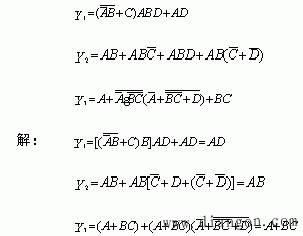
三、消项法
利用公式AB+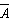 
C+BC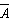=AB+ C及AB+ 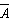C+BCD=AB+ 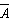C，将BC或BCD消去。其中A、B、C、D都可以是任何复杂的逻辑式。
【例】用消项法化简下列逻辑函数：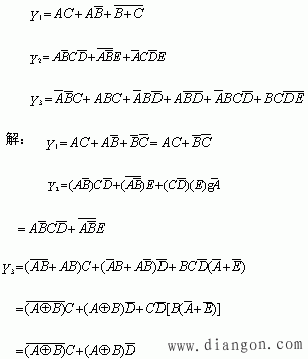
利用公式A+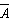B=A+B，可消去多余的因子。A、B均可以是任何复杂的逻辑式。
【例】试用消因子法化简下列逻辑函数
1、根据基本公式A+A=A可以在逻辑函数式中重复写入某一项，有时能获得更加简单的化简结果。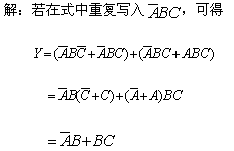
2、根据基本公式 A+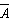=1，可以在函数式中乘以（A+ 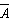），然后拆成两项分别与其他项合并，有时能得到更加简单的化简结果。
在化简复杂的逻辑函数时，往往需要灵活、交替地运用上述方法，才能得到最后的化简结果。
【例】化简逻辑函数