假定对某个被测参量进行等精度(测量误差影响程度相同)重复测量n次,其测量示值分别为X1、X2、…,Xi、…,Xn、则各次测量的测量误差,即随机误差(假定已消除系统误差)分别为
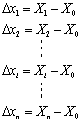 (1)
(1)
式中,X0为真值。
如果以偏差幅值(有正负)为横坐标,以偏差出现的次数为纵坐标作图。可以看出,随机误差整体上均具有下列统计特性:
(1)有界性 即各个随机误差的绝对值(幅度)均不超过一定的界限;
(2)单峰性 即绝对值(幅度)小的随机误差总要比绝对值(幅度)大的随机误差出现的概率大;
(3)对称性 (幅度)等值而符号相反的随机误差出现的概率接近相等;
(4)抵偿性 当等精度重复测量次数n→∞时,所有测量值的随机误差的代数和为零,即
![]()
所以,在等精度重复测量次数足够大时,其算术平均值![]() 就是其真值X0较理想的替代值。
就是其真值X0较理想的替代值。
大量的试验结果还表明:测量值的偏差——当没有起决定性影响的误差源(项)存在时,随机误差的分布规律多数都服从正态分布;当有起决定性影响的误差源存在,还会出现诸如均匀分布、三角分布、梯形分布、t分布等。下面对正态分布、均匀分布作简要介绍。
1.正态分布
高斯于1795年提出的连续型正态分布随机变量并的概率密度函数表达式为:
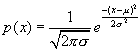 (2)
(2)
式中,μ为随机变量的数学期望值;e为自然对数的底;σ为随机变量x的均方根差或称标准偏差(简称标准差);
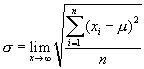 (3)
(3)
σ2为随机变量的方差,数学上通常用D表示;n为随机变量的个数。
其中,μ和σ是决定正态分布曲线的两个特征参数。其中μ影响随机变量分布的集中位置,或称其正态分布的位置特征参数;σ表征随机变量的分散程度,故称为正态分布的离散特征参数。μ值改变,σ值保持不变,正态分布曲线的形状保持不变而位置根据μ值改变而沿横坐标移动,如图2所示。当μ值不变,σ值改变,则正态分布曲线的位置不变,但形状改变,如图2所示。σ值变小,则正态分布曲线变得尖锐,表示随机变量的离散性变小;σ值变大,则正态分布曲线变平缓,表示随机变量的离散性变大。
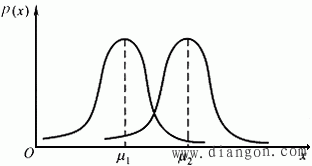
图1 μ对正态分布的影响示意图
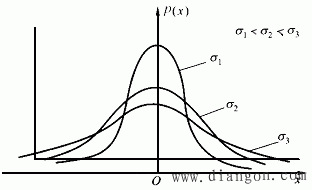
图2 σ对正态分布的影响示意图
在已经消除系统误差条件下的等精度重复测量中,当测量数据足够多时,测量的随机误差大都呈正态分布,因而完全可以参照式(1)的高斯方程对测量随机误差进行比较分析。
分析测量随机误差时,标准差d表征测量数据离散程度。σ值愈小,则测量数据愈集中,概率密度曲线愈陡峭,测量数据的精密度越高;反之,σ值愈大,测量数据愈分散,概率密度曲线愈平坦,测量数据的精密度越低。
2.均匀分布
在测试和计量中,随机误差有时还会服从非正态的均匀分布等。从误差分布图上看,均匀分布的特点是:在某一区域内,随机误差出现的概率处处相等,而在该区域外随机误差出现的概率为零。均匀分布的概率密度函数φ(x)为
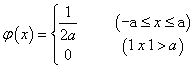 (3)
(3)
式中a为随机误差x的极限值。
均匀分布的随机误差概率密度函数的图形呈直线,如图3所示。
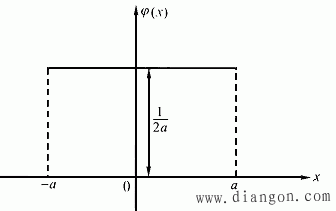
图3 均匀分布曲线
较常见的均匀分布随机误差通常是因指示式仪器度盘、标尺刻度误差造成的误差,检测仪器最小分辨力限制引起的误差,数字仪表或屏幕显示测量系统产生的量化(±1)误差,智能化检测仪器在数字信号处理中存在的舍人误差等。此外,对于一些只知道误差出现的大致范围,而难以确切知道其分布规律的误差,在处理时亦经常按均匀分布误差对待。
