定性分析就是对测量环境、测量条件、测量设备、测量步骤进行分析，看是否有某种外部条件或测量设备本身存在突变而瞬时破坏；测量操作是否有差错或等精度测量过程中是否存在其他可能引发粗大误差的因素；也可由同一操作者或另换有经验操作者再次重复进行前面的（等精度）测量，然后再将两组测量数据进行分析比较，或再与由不同测量仪器在同等条件下获得的结果进行对比，以分析该异常数据出现是否“异常”，进而判定该数据是否为粗大误差。这种判断属于定性判断，无严格的规则，应细致和谨慎地实施。
定量判断，就是以统计学原理和误差理论等相关专业知识为依据，对测量数据中的异常值的“异常程度”进行定量计算，以确定该异常值是否为应剔除的坏值。这里所谓的定量计算是相对上面的定性分析而言，它是建立在等精度测量符合一定的分布规律和置信概率基础上的，因此并不是绝对的。
下面介绍两种工程上常用的粗大误差判断准则。
1．拉伊达准则
拉伊达准则是依据对于服从正态分布的等精度测量，其某次测量误差｜Xi－X0｜大于3σ的可能性仅为0.27％。因此，把测量误差大于标准误差σ（或其估计值
）的3倍的测量值作为测量坏值予以舍弃。由于等精度测量次数不可能无限多，因此，工程上实际应用的拉伊达准则表达式为
（1）
式中，Xk为被疑为坏值的异常测量值；
为包括此异常测量值在内的所有测量值的算术平均值；为包括此异常测量值在内的所有测量值的标准误差估计值；KL（=3）为拉伊达准则的鉴别值。
当某个可疑数据Xk的
时，则认为该测量数据是坏值，应予剔除。剔除该坏值后，剩余测量数据还应继续计算3和，并按（1）式继续计算、判断和剔除其他坏值，直至不再有符合（1）式的坏值为止。
拉伊达准则是以测量误差符合正态分布为依据的，值得注意的是一般实际工程等精度测量次数大都较少，测量误差分布往往和标准正态分布相差较大；因此，在实际工程应用中当等精度测量次数较少（例如n≤20）时，仍然采用基于正态分布的拉伊达准则，其可靠性将变差，且容易造成3鉴别值界限太宽而无法发现测量数据中应剔除的坏值。可以证明，当测量次数n<10时，Xk的
总是小于3。因此，当测量次数n<10时，拉伊达准则将彻底失效，不能判别任何粗大误差。即拉伊达准则只适用于测量次数较多（例如n>25以上），测量误差分布接近正态分布的情况。
2．格拉布斯（Grubbs）准则
格拉布斯准则是以小样本测量数据，以t分布（详见概率论或误差理论有关书籍）为基础用数理统计方法推导得出的。理论上比较严谨，具有明确的概率意义，通常被认为实际工程应用中判断粗大误差比较好的准则。
格拉布斯准则是指小样本测量数据中某一测量值满足表达式
（2）
式中，Xk为被疑为坏值的异常测量值；为包括此异常测量值在内的所有测量值的算术平均值；（x）为包括此异常测量值在内的所有测量值的标准误差估计值；KG（n，α）为格拉布斯准则的鉴别值；n为测量次数；α为危险概率，又称超差概率；它与置信概率P的关系为α=1-P。
当某个可疑数据Xk的
时，则认为该测量数据是含有粗大误差的异常测量值，应予以剔除。
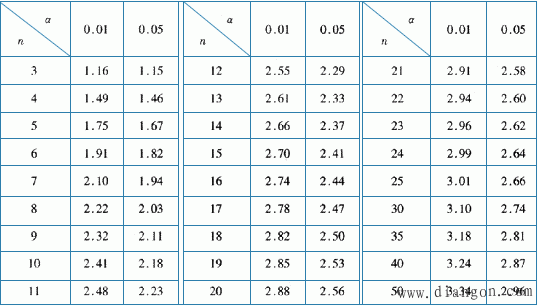
格拉布斯准则的鉴别值KG（n，α）是和测量次数n、危险概率α相关的数值，可通过查相应的数表获得。表1是工程常用α=0.05和α=0.01在不同测量次数n时，对应的格拉布斯准则鉴别值KG（n，α）表。
当α=0.05或0.01时，按测量数据个数n查表1得到格氏准则作为粗大误差的判别的鉴别值KG（n，α）的置信概率P分别为0.95和0.99。即按（2）式得出的测量值大于按表1-1查得的鉴别值KG（n，α）的可能性仅分别为0.5％和1％，这说明该数据是正常数据的概率已很小，可以认定该测量值为含有粗大误差的坏值并予以剔除。
表1 KG （n，α）数值表
应注意的是，若按式（1-22）和表1-1查出多个可疑测量数据时，不能将它们都作为坏值一并剔除，每次只能舍弃误差最大的那个可疑测量数据，如误差超过鉴别值KG（n，α）最大的两个可疑测量数据数值相等，也只能先剔除一个，然后按剔除后的测量数据序列重新计算、（x）并查表获得新的鉴别值KG（n-1，α），重复进行以上判别，直到判明无坏值为止。
格拉布斯准则是建立在统计理论基础上，对n<30的小样本测量较为科学、合理的判断粗大误差的方法。因此，目前国内外普遍推荐使用此法处理小样本测量数据中的粗大误差。
如果发现在某个测量数据序列中，先后查出的坏值比例太大，则说明这批测量数据极不正常，应查找和消除故障后重新进行测量和处理。