一、代数法
在n变量的逻辑函数表达式中,给n-1个变量以特定取值(0或1)后,表达式中仅保留某个具有竞争能力的变量x,使逻辑函数表达式变成x+ 或者x· 的形式,则实现该表达式的电路存在冒险。
例5.3.1 已知逻辑电路图如图5.3.8(a)所示,判断电路是否存在冒险,并画出消除冒险的电路。
解:根据图5.3.8(a)的电路图写出F= =AB+ C。令B=C=1时,F=A+ ,所以会产生0冒险。
消除冒险的方法是消除A+ 产生的条件,即根据包含律将F改写为F=AB+ C+BC。令B=C=1时,F=A+ +1=1,不可能出现0冒险,画出电路图如图5.3.8(b)所示。

二、卡诺图法
在逻辑函数的卡诺图中,函数的每个与项(或者或项)对应卡诺图上一个卡诺圈,若两个卡诺圈相切,相切处将会发生冒险。
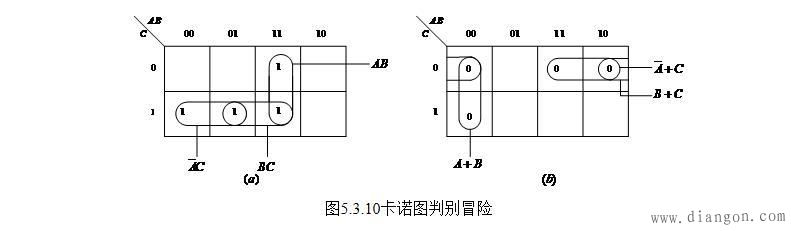
图5.3.10(a)为例5.3.1中F=AB+ C的卡诺图,图5.3.10(b)为例5.3.2中F=(A+B)( +C)的卡诺图。
从图5.3.10(a)看出AB和 C两个卡诺图相切处B=C=1,当A变化时产生冒险,与代数法结论一致。从图5.3.10(b)看出, +C和A+B两个卡诺圈相切处B=C=0,当A发生变化时将产生冒险。要消除上述冒险只要在相切部分增加一个卡诺圈,即可消除相切部分的冒险。增加卡诺圈后图5.3.10(a)的函数F=AB+ C+BC,图5.3.10(b)的函数F=(A+B)( +C)(B+C)与代数法结论一致。实现的电路图同图5.3.8(b)和图5.3.9(b)。
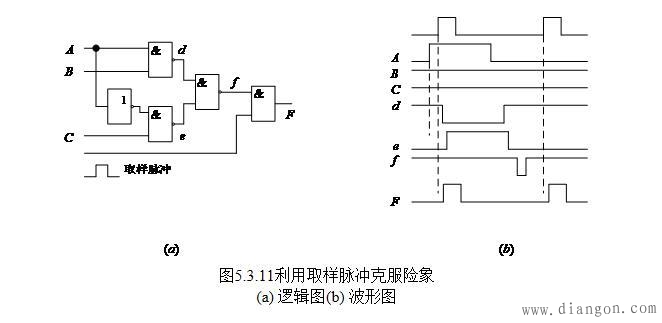
三、取样脉冲法
一般说来,多个输入发生状态变化时,冒险是难以完全消除的,当组合电路的冒险影响了整个系统的工作时,可以用取样的方法解决。取样脉冲仅在输出处于稳定值的期间到来,以保证输出正确的结果,如图5.3.11所示。在没有取样脉冲期间,输出端的信息是无效的。
四、输出端加滤波电路
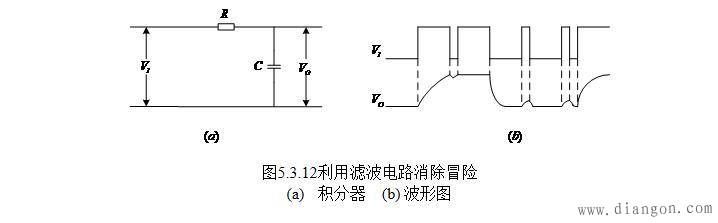
为了滤除毛刺,在组合电路输出端加一积分器,RC积分器是一低通滤波器,能滤除信号中的高频分量,而组合逻辑电路所产生的毛刺是一个低频分量少而有丰富高频分量的信号。这种信号通过低通滤波器后基本上把毛刺滤掉,能保留下消除了毛刺的较为平滑的信号,如图5.3.12(b)所示,图中VI为组合电路的输出。
在使用滤波电路时要正确选择时常数τ=RC,它要比毛刺的宽度大,大到足以吸收掉毛刺但也不能太大以免使信号形状出现不能允许的畸变,一般都是通过实验确定RC的值。