一、定义及应用范围：
• 定义：以电路中各个结点对参考点电压 ( 结点电压 ) 为未知量，根据 KCL 对结点列结点电流方程，根据求解出各结点电压，从而求出各元件上的电压、电流。
• 适用范围： 电路中的独立结点数少于独立回路数时，用结点电压法比较方便、方程个数较少。
• 验证：如下图所示电路
• 
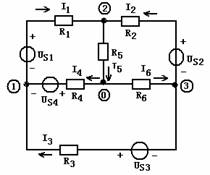选定一个参考结点，记为 0 ，则各结点参考点之间的电压 
、 
、 
为未知量。
• 列结点电流方程：
• 对结点 ①有： 
；
对结点②有： 
；
对结点③有： 
• 利用欧姆定律和 KVL 列写支路电流与结点电压关系式：
• 将第（ 4 ）步中各支路电流代入方程 ①②③ 中，得：
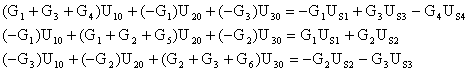
二、解题步骤及注意事项：
• 选取独立结点和参考结点，则独立结点到参考结点间的电压为结点电压
• 对 n 个结点的电路，能列 (n-1) 个结点电压方程。
• 以结点电压为独立变量根据 KCL 列写独立结点的结点电流方程，方程的左边是无源元件电流的代数和，自导上的电流恒为 “ + ” ，互导上的电流为 “ - ” ；方程右边为独立电流源的代数和，当电流源的正方向指向该结点时取 “+” ，反之取 “ － ” 。结点电压方程的一般表达形式为：
自导 ×本结点电压 + 
= 流入该结点的所有电源的电流之和。
①自导： ( 自电导 ) ，其值总为正的，是指与某结点相连的所有电导之和；※理想电流源串联的电导不能计算在内。
②互导：指相邻两结点之间的公共电导之和，互导总为负 ；与理想电流串联的电导不能计算在内。
③ 流入结点的所有电源电流之和，包括两层含义： a 是电源电流流入结点的取“ + ”，流出结点的取“－”； b 是该电流必须是电源的电流，即可以是电流的电流，还可以是电压源的电流，还可以是受控源的电流，但不能是非电源支路的电流。
三、弥尔曼定理：只有两个结点的结点电压法。
通式： 
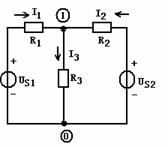
例 ： 用结点电压法求解如下图所示电路中的各支路电流。
解： 此题只有两个结点，所以可用弥尔曼定理。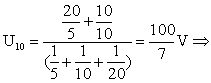 
