1、:通用方法,不改变电路结构,列方程求解。不适用支路数多的电路。
2、:改变电路的结构。理想电压源、理想电流源之间不能互换。
3、:电阻的串、并联等效化简。
4、:适用线性电路。不适用电源个数较多的电路。
5、:适用线性电路。适用求某条支路上的电流或两端电压。
二、举例
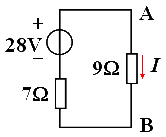
例:求图示电路中A,B支路中的电流I。
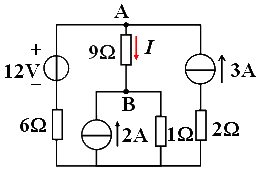 此题我们准备用多种方法来求解,对于每一种方法,大家应熟悉方法的内容和解题步骤。
此题我们准备用多种方法来求解,对于每一种方法,大家应熟悉方法的内容和解题步骤。解:(1)采用支路电流法求解。
分析:电路支路数b=5,结点数n=3;其中有两条支路中含有电流源。实际未知的支路电流为3,因此只需列3个方程。
将待求支路电流在图中标出,在选择回路时应避开含有电流源支路的回路,标出回路绕向。
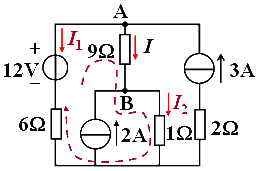 列方程组得
列方程组得用支路电流法求解,列KCL和KVL方程是关键,特别注意KVL方程容易列错。此方法的难点在于解方程组,优点在于可以一下算出所有支路的电流。
(2)采用实际电源模型的等效变换化简求解
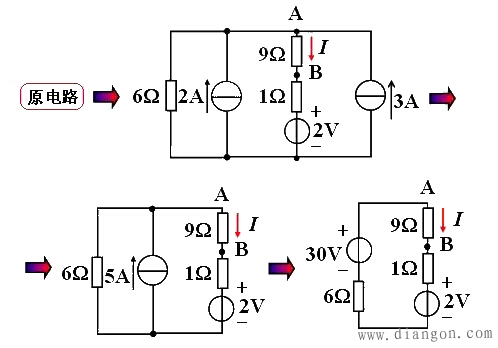
16I+2-30=0
I=1.75A
用实际电源模型的等效变换来化简电路,每一步化简都应画出相应的电路图,直到将电路化成一个单回路电路或者是一个电流源并联两个电阻的电路。注意在化简过程中,待求支路一般不参与化简。此种方法的缺点在于需画若干个电路,优点在于只要清楚了实际电压源和实际电流源的等效参数变换,整个化简过程都是重复应用。
(3)采用叠加原理求解
解:① 12V电压源单独作用,电路如图所示。
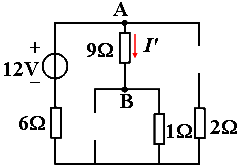
②2A电流源单独作用,电路如图所示。
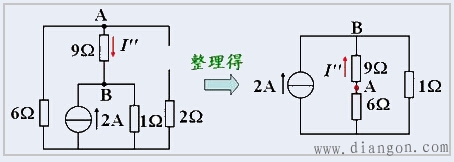
③3A电流源单独作用,电路如图所示。
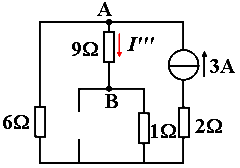
④求I。
用叠加原理来求解未知量,每个电源单独作用时的电路图应该画出。该方法的优点在于将多个电源共同作用的电路,化成每个电源单独作用的电路,这实际上也改变了电路的结构,便于求出未知量;缺点在于,对于每一个电路都要重新分析、计算,工作量较大。
(4)采用戴维宁定理求解
解:(1)求Uoc。
去掉待求支路,得有源线性二端网络。
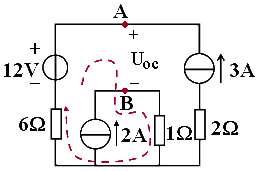
(2)求Req。
将(1)中的有源线性二端网络除源(电压源短路、电流源开路),得到无源线性二端网络。
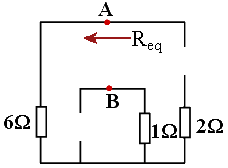
(3)求I。
将有源线性二端网络的戴维宁等效电路并在去掉的支路两端,形成一个单回路电路。
此方法适用于求一条支路的电流或两端电压。将待求支路从原电路中拿掉,实际上也改变了电路结构,此时得到的有源线性二端网络一定要单独画出,不要在原电路中求开路电压。该方法的优点在于将复杂电路简化成一个单回路电路,难点在于求等效电压源时,方法有多种选择,具有一定的难度。
