描述正弦量的三要素

描述正弦量的数学表达式：i=Imsin(ωt+φ)
　　下面是正弦量的波形图 　

　　（1）频率f、周期Τ和角频率ω：表示正弦量变化的快慢。
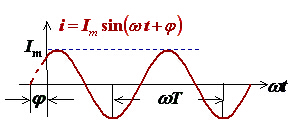
　　①周期
　　表示正弦量变化一次所需的时间，规定用字母T来表示，单位是秒（s）。
　　②频率
　　表示正弦量在单位时间内重复变化的次数，规定用字母f来表示，单位是赫兹（Hz）。
　　③角频率
　　交流电量在一个周期T内变化的角度是2л个弧度，将交流电在1秒内变化的弧度数称为交流电的角频率，用ω来表示，单位是弧度/秒（rad/s）。
　　三者关系为
　　我国及世界上许多国家工业电网所采用的交流电频率是50Hz，这种频率的交流电又称为工频交流电。
　　当频率很高时，可用千赫（kHz）或兆赫（MHz）作单位。
　　换算关系是 1MHz=103kHz=106Hz
　　无线电广播信号中波段的频率从535kHz到1605kHz，电视广播和手机通讯信号的频率高达几十到几千兆赫兹。
　　（2）有效值和幅值：表示正弦量的大小。
　　瞬时值：任意时刻交流量的大小，有正值、负值。
　　幅值或最大值：瞬时值中的最大正值。
　　有效值是根据交流电流和直流电流具有相等的热效应来定义的。
　　有效值：在交流电变化的一个周期内，交流电流在电阻R上产生的热量相当于多大数值的直流电流在该电阻上所产生的热量，此直流电流的数值就是该交流电流的有效值。
　　i=Imsin(ωt+φ)
　　→
　　同理：，。
　　注意：交流仪表测得的电压、电流的数值是有效值。
　　区别各量的表达方式：
　　瞬时值：用表示。
　　幅值或最大值：用，，表示。
　　有效值：用U，E，I表示。
　　注意：交流电的有效值和最大值都有实用意义。当考虑能量转化时要用有效值；当考虑用电器的绝缘性能时要用最大值。
　　（3）相位和初相位
　　①相位角或相位：任意瞬间的电角度ωt+φ。反映了正弦量在t时刻所处的状态，当相位角随时间连续的变化时，正弦量的瞬时值也随之作连续的变化。
　　②初相角或初相位：t＝0时的相位，用符号φ来表示。它反映了正弦量在初始时刻所处的状态。
　　初相角在波形图形中的计算方法是：
　　变化起点：正弦量的瞬时值由负变正过程中，与横坐标相交的点。
　　变化起点在纵坐标的左面，则φ为正，在右边为负。
　　在下图中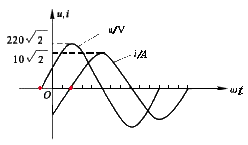，，。 　　 　　初相角与计时起点有关，不同的计时起点，对应于不同的初相角。同一电路中有许多相关的正弦量时，只能取一个共同的计时起点，从而确定各自的初相位。
　　取值范围：
　　③相位差：描述两个同频率的正弦交流电在任何瞬时的相位之差。
　　
　　
　　相位差等于初相位之差，不随计时起点而变。
　　同相：,表示u与i同相。
　　反相：，表示u与i反向。
　　超前：表示u超前于i。
　　滞后：表示u滞后于i。
　　在同一个周期内，一个正弦量比另一个正弦量早些或晚些到达最大值，前者被称为超前，后者被称为滞后。
　　如果两个同频率的正弦量同时达到最大值，则这两个正弦量称为同相。
　　如果两个同频率正弦量同时达到零值，但当一个达到正的最大值时，另一个达到负的最大值，则这两个正弦量的相位互差180°，称为反相。
　　注意：超前和滞后的概念是相对的。
　　相位差可以通过观察波形来确定，方法是：在波形图中确定同一个周期内两个波形的最大值之间的角度差，即为两者的相位差。在波形图中，先到达最大值的为超前，后到达最大值的为滞后。