检测系统静态特性的主要参数

　　静态特性表征检测系统在被测参量处于稳定状态时的输出-输入关系。衡量检测系统静态特性的主要参数是指测量范围、精度等级、灵敏度、线性度、滞环、重复性、分辨力、灵敏限、可靠性等。

　　1．测量范围

　　每个用于测量的检测仪器都有规定的测量范围，它是该仪表按规定的精度对被测变量进行测量的允许范围。测量范围的最小值和最大值分别称为测量下限和测量上限，简称下限和上限。仪表的量程可以用来表示其测量范围的大小，用其测量上限值与下限值的代数差来表示，即

量程=|测量上限值-测量下限值|　　　　　　　　（1）

　　用下限与上限可完全表示仪表的测量范围，也可确定其量程。如一个温度测量仪表的下限值是-50℃，上限值是150℃，则其测量范围（量程）可表示为

量程=|150℃-（-50℃）|=200℃

　　由此可见，给出仪表的测量范围便知其测量上下限及量程，反之只给出仪表的量程，却无法确定其上下限及测量范围。

　　2．精度等级

　　检测仪器及系统精度等级，在第一节三中已描述，这里不再重述。

　　3．灵敏度

　　灵敏度是指测量系统在静态测量时，输出量的增量与输入量的增量之比。即

　　　　　　　　　　　　　　（2）

　　对线性测量系统来说，灵敏度为：

　　　　　　　　　　　　　　（3）

　　亦即线性测量系统的灵敏度是常数，可由静态特性曲线（直线）的斜率来求得，如图1（a）所示，式中，m_y、m_x为y轴和x轴的比例尺，θ为相应点切线与x轴间的夹角。非线性测量系统的灵敏度是变化的，如图1（b）所示。

　　对非线性测量系统来说，其灵敏度由静态特性曲线上各点的斜率来决定。

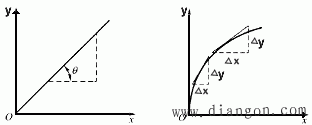
（a）线性系统灵敏度示意图 （b）非线性系统灵敏度示意图

图1　灵敏度示意图

　　灵敏度的量纲是输出量的量纲和输入量的量纲之比。

　　4．线性度

　　线性度通常也称为非线性度。理想的测量系统，其静态特性曲线是一条直线。但实际测量系统的输入与输出曲线并不是一条理想的直线。线性度就是反映测量系统实际输出、输入关系曲线与据此拟合的理想直线y（x）=a₀+a₁x并的偏离程度。通常用最大非线性引用误差来表示。即

　　　　　　　　　　　　　（4）

　　由于最大偏差是以拟合直线为基准计算的，因此拟合直线确定的方法不同，则不同，测量系统线性度也不同。所以，在表示线性度时应注意要同时说明具体采用的拟合方法。选择拟合直线，通常以全量程多数测量点的非线性误差都相对较小的为佳。常用的拟合直线方法有理论直线法、端基线法和最dxz乘法等，与之相对应的即是理论线性度、端基线性度和最小二乘法线性度等。实际工程中多采用理论线性度和最小二乘法线性度。

　　（1）理论线性度及其拟合直线

　　理论线性度也称绝对线性度。它以测量系统静态理想特性y（x）=kx作为拟合直线，如图2中的直线l（曲线2为系统全量程多次重复测量平均后获得的实际输出一输入关系曲线，曲线3为系统全量程多次重复测量平均后获得的实际测量数据，采用最小二乘法方法拟合得到的直线）。此方法优点是简单、方便和直观；缺点是多数测量点的非线性误差相对都较大（△L₁为该直线与实际曲线在某点的偏差值）。

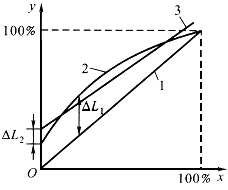
图2　最小二乘和理论线性度及其拟合直线

　　（2）最小二乘线性度及其拟合直线

　　最小二乘法方法拟合直线方程为y（x）=a₀+a₁x如何科学、合理地确定系数a₀和a₁是解决问题的关键。设测量系统实际输出一输入关系瞌线上某点的输入、输出分别x_i、y_i在输入同为x_i情况下，最小二乘法拟合直线上得到输出值为y（x_i）= a₀+a₁x_i，两者的偏差为

　　最小二乘拟合直线的原则是使确定的n个特征测量点的均方差为最小值，因

（5）

　　为此必有f（a₀，a₁）对a₀和a₁的偏导数为零，即

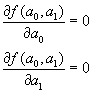
　　把f（a₀，a₁）的表达式代入上述两方程，整理可得到关于最小二乘拟合直线的待定系数a₀和a₁的两个表达式

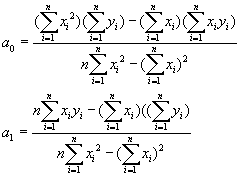　　　　（6）

　　（图2中△L₂为最小二乘拟合曲线与实际曲线在某点的偏差值）

　　5．迟滞

　　迟滞，又称滞环，它说明传感器或检测系统的正向（输入量增大）和反向（输入量减少）输入时输出特性的不一致程度，亦即对应于同一大小的输入信号，传感器或检测系统在正、反行程时的输出信号的数值不相等，见图3所示。

　　迟滞误差通常用最大迟滞引用误差来表示，即

　　　　　　　　　　　　　（7）

　　式中，为最大迟滞引用误差；为（输入量相同时）正反行程输出之间的最大绝对偏差；为测量系统满量程值

　　在多次重复测量时，应以正反程输出量平均值间的最大迟滞差值来计算。迟滞误差通常是由于弹性元件、磁性元件以及摩擦、间隙等原因所引起的，一般需通过具体实测才能确定。

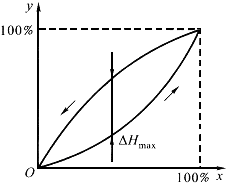
图3　迟滞特性示意图

　　6．重复性

　　重复性表示检测系统或传感器在输入量按同一方向（同为正行程或同为反行程） 作全量程连续多次变动时所得特性衄线的不一致程度，如图4所示。

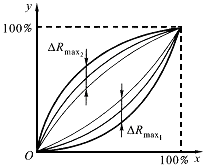
图4　检测系统重复性示意图

　　特性曲线一致性好，重复性就好，误差也小。重复性误差是属于随机误差性质的，测量数据的离散程度是与随机误差的精密度相关的，因此应该根据标准偏差来计算重复性指标。重复性误差d。可按下式计算：

　　　　　　　　　　　　　　（8）

　　式中，为重复性误差；Z为置信系数，对正态分布，当Z取2时，置信概率为95％，Z取3时，概率为99．73％；对测量点和样本数较少时，可按t分布表选取所需置信概率所对应的置信系数。为正、反向各测量点标准偏差的最大值；为测量系统满量程值。

　　式（8）中标准偏差的计算方法可按贝塞尔公式计算。按贝塞尔公式计算，通常应先算出各个校准级上的正、反行程的子样标准偏差，即

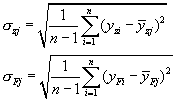　　　　　　　　　　（9）

　　式中，为第j次测量正行程和反行程测量数据的子样标准偏差（j=1，2，…，m）；、为第j次测量上正行程和反行程的第i个测量数据（i=1，2，…，n）；、为第j次测量上正行程和反行程测量数据的算术平均值。

　　取上述正反行程σ共2m个测量点）中的最大值及所选置信系数和量程便可按式（8）计算，得到测量系统的重复性误差。

　　计算标准偏差还有一种较常见的方法——极差（测量数据最大值与最小值之差）法，它是以正、反行程极差平均值和极差系数来计算标准偏差。限于篇幅，这里从略。

　　7．分辨力

　　能引起输出量发生变化时输入量的最小变化量称为检测系统的分辨力。例如，线绕电位器的电刷在同一匝导线上滑动时，其输出电阻值不发生变化，因此能引起线绕电位器输出电阻值发生变化的（电刷）最小位移△X为电位器所用的导线直径，导线直径越细，其分辨力就愈高。许多测量系统在全量程范围内各测量点的分辨力并不相同，为统一，常用全量程中能引起输出变化的各点最小输入量中的最大值相对满量程输出值的百分数来表示系统的分辨力。即

　　　　　　　　　　　　　　　　　　（10）

　　8．死区

　　死区又叫失灵区、钝感区、阈值等，它指检测系统在量程零点（或起始点）处能引起输出量发生变化的最小输入量。通常均希望减小失灵区，对数字仪表来说失灵区应小于数字仪表最低位的二分之一。

　　9．可靠性

　　通常，检测系统的作用是不仅要提供实时测量数据，而且往往作为整个自动化系统中必不可少的重要组成环节而直接参与和影响生产过程控制。因此，检测系统一旦出现故障就会导致整个自动化系统瘫痪，甚至造成严重的生产事故，为此必须十分重视检测系统的可靠性。衡量检测系统可靠性的指标有：

　　（1）平均无故障时间MTBF（Mean Time Between Failure）指检测系统在正常工作条件下开始连续不间断工作，直至因系统本身发生故障丧失正常工作能力时为止的时间，单位通常为小时或天。

　　（2）可信任概率P表示在给定时间内检测系统在正常工作条件下保持规定技术指标（限内）的概率。

　　（3）故障率故障率也称失效率，它是平均无故障时间MTBF的倒数。

　　（4）有效度 衡量检测系统可靠性的综合指标是有效度，对于排除故障，修复后又可投入正常工作的检测系统，其有效度A定义为平均无故障时间与平均无故障时间、平均故障修复时间MTFR（Mean Time To Repair）和的比值，即

　　　　　　　　　　　　　（11）

　　对于使用者来说，当然希望平均无故障时间尽可能长，同时又希望平均故障修复时间尽可能的短，也即有效度的数值越大越好。此值越接近1，检测系统工作越可靠。

　　以上是检测系统的主要技术指标，此外检测系统还有经济方面的指标，如功耗、价格、使用寿命等。

　　检测系统使用方面的指标有：操作维修是否方便，能否可靠安全运行以及抗干扰与防护能力的强弱，重量、体积的大小，自动化程度的高低等。