检测系统的动态特性的数学模型主要有三种形式：时域分析用的微分方程；频域分析用的频率特性；复频域用的传递函数。测量系统动态特性由其本身各个环节的物理特性决定，因此如果知道上述三种数学模型中的任一种，都可推导出另外两种形式的数学模型。
1．微分方程
对于线性时不变的测量系统来说，表征其动态特性的常系数线性微分方程式为
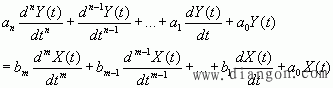（1）
式中，Y（t）为输出量或响应；X（t）为输入量或激励；
为与测量系统结构的物理参数有关的系数；
为输出量Y对时间t的n阶导数；
为输入量X对时间t的m阶导数。
由式（1）可以求出在某一输入量作用下测量系统的动态特性。但是对一个复杂的测量系统和复杂的被测信号，求该方程的通解和特解颇为困难，往往采用传递函数和频率响应函数更为方便。
2．传递函数
若测量系统的初始条件为零，则把测量系统输出（响应函数）Y（t）的拉氏变换Y（s）与测量系统输入（激励函数）X（t）的拉氏变换X（s）之比称为测量系统的传递函数H（s）。
假定在初始t=0时，满足输出Y（t）=0和输入X（t）=0，以及它们对时间的各阶导数的初始值均为零的初始条件，这时Y（t）和X（t）的拉氏变换Y（s）和x（s）计算公式为
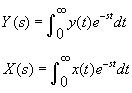（2）
满足上述初始条件时，对（1）式两边取拉氏变换，就得测量系统的传递函数
（3）
上式分母中s的最高指数n即代表微分方程的阶数，相应地当n=1，n=2则称为一阶系统传递函数和二阶系统传递函数。由式（3）可得：
Y（s）=H（s）·X（s） （4）
知道测量系统传递函数和输入函数即可得到输出（测量结果）函数Y（s），然后利用拉氏反变换，求出Y（s）的原函数，即瞬态输出响应为
y（t）=L-1[Y（s）] （5）
传递函数具有以下特点：
（1）传递函数是测量系统本身各环节固有特性的反映，它不受输入信号影响，但包含瞬态、稳态时间和频率响应的全部信息
（2）传递函数H（s）是通过把实际测量系统抽象成数学模型后经过拉氏变换得到的，它只反映测量系统的响应特性。
（3）同一传递函数可能表征多个响应特性相似，但具体物理结构和形式却完全不同的设备，例如一个RC滤波电路与有阻尼弹簧的响应特性就类似，它们同为一阶系统。
3．频率（响应）特性
在初始状态为零的条件下，把测量系统的输出Y（t）的傅里叶变换Y （jω）与输入X（t）的傅里叶变换X （jω）之比称为测量系统的频率响应特性，简称频率特性。通常用H（jω）来表示。
对稳定的常系数线性测量系统，可取s=jω，即令其实部为零，这样式（2）就变为
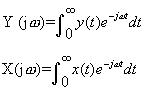（6）
根据式（6）或直接由式（3）转换得到测量系统的频率特性n（jω）
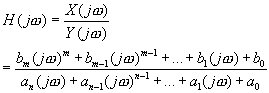（7）
从物理意义上说，通过傅里叶变换可将满足一定初始条件的任意信号分解成一系列不同频率的正弦信号之和（叠加），从而将信号由时域变换至频率域来分析。因此频率响应函数是在频率域中反映测量系统对正弦输入信号的稳态响应，也被称为正弦传递函数。
传递函数表达式（3）和频率特性表达式（6）形式相似，但前者是测量系统输出与输入信号的拉氏变换式之比，其输入并不限于正弦信号，所反映的系统特性不仅有稳态也包含瞬态；后者仅反映测量系统对正弦输入信号的稳态响应。
对线性测量系统其稳态响应（输出）是与输入（激励）同频率的正弦信号。对同一正弦输入，不同测量系统稳态响应的频率虽相同，但幅度和相位角通常不同。同一测量系统当输入正弦信号的频率改变时，系统输出与输入正弦信号幅值之比随（输入信号）频率变化关系称为测量系统的幅频特性，通常用A（ω）表示；系统输出与输入正弦信号相位差随（输入信号）频率变化的关系称为测量系统的相频特性，通常用ф（ω）表示。幅频特性和相频特性合起来统称为测量系统的频率（响应）特性。根据得到的频率特性可以方便地在频率域直观、形象和定量地分析研究测量系统的动态特性。