1、逐点比较法直线插补
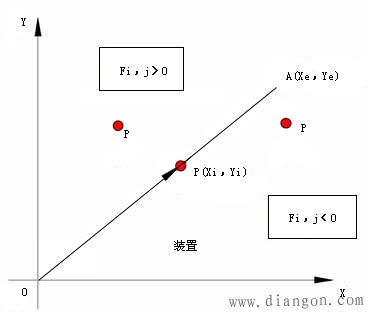
第Ⅰ象限一加工直线,起点坐标原点O,终点坐标为A(xe,ye),则直线方程可表示为
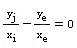 ,即
,即 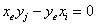
令Fi,j=xeyj-yexi为偏差判别函数,则有:
(1)当Fi,j≥0时,向+X方向进给一个脉冲当量,到达点 Pi+1,j,此时xi+1=xi+1,则点Pi+1,j的偏差判别函数Fi+1,j为
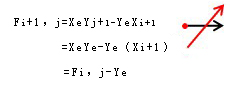
(2)当Fi,j<0时,向+Y方向进给一个脉冲当量,到达点Pi,j+1,此时yj+1=yj+1,则点Pi,j+1的偏差判别函数Fi,j+1为

可见,新加工点的偏差Fi+1,j或Fi,j+1是由前一个加工点的偏差Fi,j和终点的坐标值递推出来的,如果按前两式计算偏差,则计算大为简化。
终点判别三种方法:
(1)判别插补或进给的总步数:N=Xe+Ye;
(2)分别判别各坐标轴的进给步数;
(3)仅判断进给步数较多的坐标轴的进给步数。
总结:
|
第一拍判别 |
第二拍判别 |
第三拍判别 |
第四拍比较 |
|
Fij≥0 |
+Δx |
Fi+1,j= Fi,j-ye |
Ei+j=E终-1 |
|
Fij<0 |
+Δy |
Fi,j+1= Fi,j+xe |
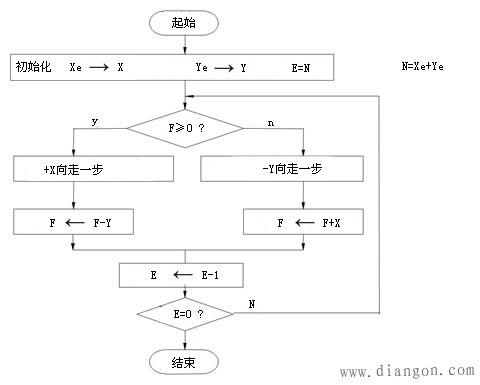
第Ⅰ象限直线插补流程图:
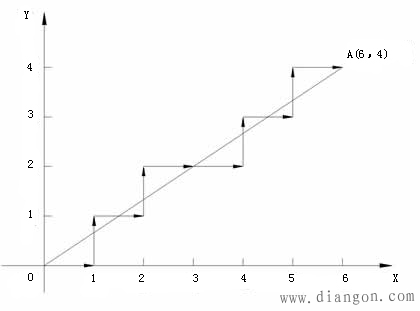
例5-1 设加工第一象限直线,起点为坐标原点O(0,0),终点A(6,4),用逐点比较法对其进行插补,并画出插补轨迹。
终点判别寄存器E=6+4=10,每进给一步减1,E=0时停止插补。
|
步数 |
偏差判别 |
坐标进给 |
偏差计算 |
终点判别 |
|
起点 |
F0,0=0 |
E=10 | ||
|
1 |
F0,0=0 |
+X |
F1,0=F0,0-ye=0-4=-4 |
E=10-1=9 |
|
2 |
F1,0<0 |
+Y |
F1,1= F1,0+xe=-4+6=2 |
E=9-1=8 |
|
3 |
F1,1>0 |
+X |
F2,1= F1,1-ye=2-4=-2 |
E=8-1=7 |
|
4 |
F2,1<0 |
+Y |
F2,2= F2,1+xe=-2+6=4 |
E=7-1=6 |
|
5 |
F2,2>0 |
+X |
F3,2= F2,2-ye=4-4=0 |
E=6-1=5 |
|
6 |
F3,2=0 |
+X |
F4,2= F3,2-ye=0-4=-4 |
E=5-1=4 |
|
7 |
F4,2<0 |
+Y |
F4,3= F4,2+xe=-4+6=2 |
E=4-1=3 |
|
8 |
F4,3>0 |
+X |
F5,3= F4,3-ye=2-4=-2 |
E=3-1=2 |
|
9 |
F5,3<0 |
+Y |
F5,4= F5,3+xe=-2+6=4 |
E=2-1=1 |
|
10 |
F5,4>0 |
+X |
F6,4= F5,4-ye=4-4=0 |
E=1-1=0 |
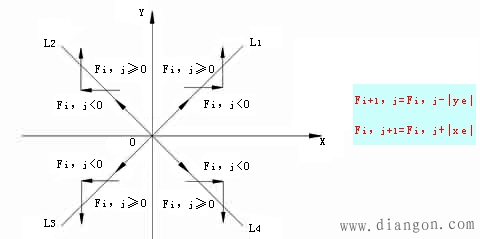
2、其他象限直线插补的方法:
1)分别处理法
分别建立其他三个象限偏差函数计算公式。脉冲进给方向由实际象限决定。
2)坐标变换法(常用)
经坐标变换,按第一象限偏差函数计算公式计算;进给脉冲方向则由实际象限决定。其他各象限直线点的坐标取绝对值,这样,插补计算公式和流程图与第一象限直线一样。