直线函数法是典型的数据采样插补方法之一。
采用时间分割思想,根据编程的进给速度将轮廓曲线分割为每个插补周期的进给直线段(又称轮廓步长)进行数据密化,以此来逼近轮廓曲线。
着重解决两个问题——
(1)如何选择插补周期T;
(2)如何计算在一个插补周期内各坐标轴的增量值△x或△y。
T与采样周期T反馈可相同或不同,一般
T=T反馈的整数倍
直线函数法特点:算法简单、计算速度快、插补误差小、精度高。
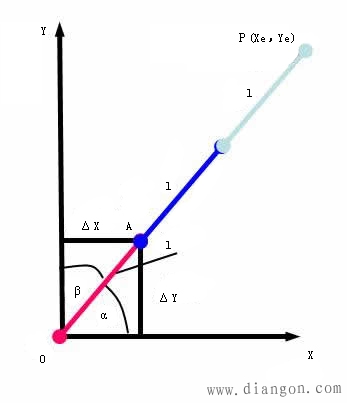
1、直线函数法直线插补
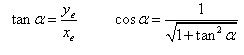
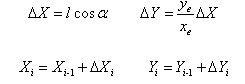
2、直线函数法圆弧插补
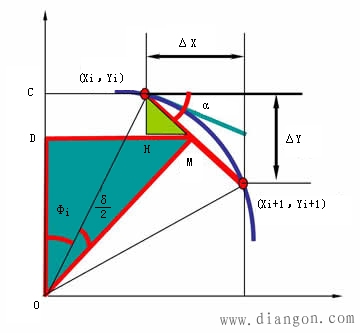
在圆弧插补时,以内接弦进给代替弧线进给。
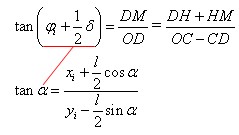
采用sin45°和cos45°来取代sinα和cosα近似求解tanα,这样造成的tanα的偏差最小,即
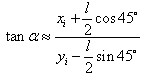
再由关系式
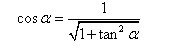
进而求得
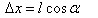
△y的计算不能采用△y= lsinα计算,而采用下式计算
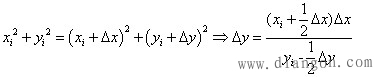
因此,求新的插补点坐标
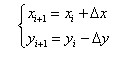
采用近似计算引起的偏差能够保证圆弧插补的每一插补点位于圆弧轨迹上,仅造成每次插补轮廓步长l的微小变化,所造成的进给速度误差<指令速度的1﹪,这种变化在加工中是允许的,完全可认为插补速度仍是均匀的。
