一、数学模型建立
机械系统的数学模型建立与电气系统数学模型建立基本相似,都是通过折算的办法将复杂的结构装置转换成等效的简单函授关系,数学表达式一般是线性微分方程(通常简化成二阶微分方程)。机械系统的数学模型分析的是输入(如电机转子运动)和输出(如工作台运动)之间的相对关系。等效折算过程是将复杂结构关系的机械系统的惯量、弹性模量和阻尼(或阻尼比)等机械性能参数归一处理,从而通过数学模型来反映各环节的机械参数对系统整体的影响。
下面以数控机床进给传动系统为例,来介绍建立数学模型的方法。在图1所示的数控机床进给传动系统中,电动机通过两级减速齿轮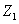 、
、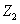 、
、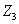 、
、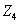 及丝杠螺母副驱动工作台作直线运动。设
及丝杠螺母副驱动工作台作直线运动。设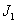 为轴I部件和电动机转子构成的转动惯量;
为轴I部件和电动机转子构成的转动惯量;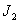 、
、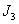 为轴Ⅱ、Ⅲ部件构成的转动惯量;
为轴Ⅱ、Ⅲ部件构成的转动惯量;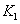 、
、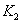 、
、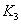 分别为轴I、Ⅱ、Ⅲ的扭转刚度系数;K为丝杠螺母副及螺母底座部分的轴向刚度系数;m为工作台质量;C为工作台导轨粘性阻尼系数:
分别为轴I、Ⅱ、Ⅲ的扭转刚度系数;K为丝杠螺母副及螺母底座部分的轴向刚度系数;m为工作台质量;C为工作台导轨粘性阻尼系数: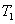 、
、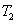 、
、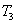 分别为轴I、Ⅱ、Ⅲ的输入转矩。
分别为轴I、Ⅱ、Ⅲ的输入转矩。
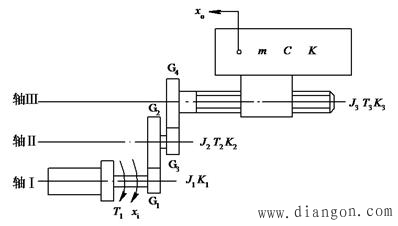
图1 数控机床进给系统
建立该系统的数学模型,首先是把机械系统中各基本物理量折算到传动链中的某个元件上(本例折算到轴I上),使复杂的多轴传动关系转化成单一轴运动,转化前后的系统总机械性能等效;然后,在单一轴基础上根据输入量和输出量的关系建立它的输入/输出的数学表达式(即数学模型)。根据该表达式进行的相关机械特性分析就反映了原系统的性能。(http://www.ippipp.com/版权所有)在该系统的数学模型建立过程中,我们分别针对不同的物理量(如J、K、ω)求出相应的折算等效值。
机械装置的质量(惯量)、弹性模量和阻尼等机械特性参数对系统的影响是线性叠加关系,因此在研究各参数对系统影响时,可以假设其它参数为理想状态,单独考虑特性关系。下面就基本机械性能参数,分别讨论转动惯量、弹性模量和阻尼的折算过程。
1、转动惯量的折算
把轴I、Ⅱ、Ⅲ上的转动惯量和工作台的质量都折算到轴I上,作为系统的等效转动惯量。设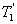 、
、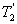 、
、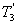 分别为轴I、Ⅱ、Ⅲ的负载转矩,ω1、ω2、ω3分别为轴I、Ⅱ、Ⅲ的角速度;υ为工作台位移时的线速度。
分别为轴I、Ⅱ、Ⅲ的负载转矩,ω1、ω2、ω3分别为轴I、Ⅱ、Ⅲ的角速度;υ为工作台位移时的线速度。
(1)I、Ⅱ、Ⅲ轴转动惯量的折算 根据动力平衡原理,I、Ⅱ、Ⅲ轴的力平衡方程分别是:
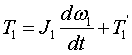 (1)
(1)
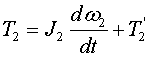 (2)
(2)
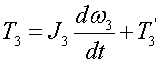 (3)
(3)
因为轴Ⅱ的输入转矩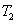 是由轴I上的负载转矩获得,且与它们的转速成反比,所以
是由轴I上的负载转矩获得,且与它们的转速成反比,所以
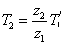
又根据传动关系有 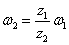
把T2和ω2值代入式3,并将式2中的T1也带入,整理得
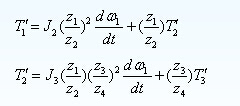
(2)工作台质量折算到I轴 在工作台与丝杠间,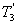 驱动丝杠使工作台运动。
驱动丝杠使工作台运动。
根据动力平衡关系有
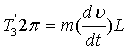
式中υ——工作台线速度;
L——丝杠导程。
即丝杠转动一周所做的功等于工作台前进一个导程时其惯性力所做的功。
又根据传动关系有
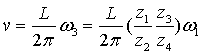
把v值代入上式整理后得
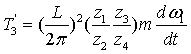 (4)
(4)
(3)折算到轴Ⅰ上的总转动惯量 把式(2)、(3)、(4)代入式(1)(2)(3),消去中间变量并整理后求出电机输出的总转矩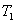 为
为
 (5)
(5)
式中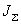 =
=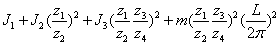 (6)
(6)
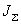 为系统各环节的转动惯量(或质量)折算到轴I上的总等效转动惯量。其中
为系统各环节的转动惯量(或质量)折算到轴I上的总等效转动惯量。其中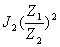 、
、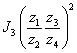 、
、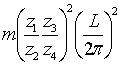 分别为Ⅱ、Ⅲ轴转动惯量和工作台质量折算到I轴上的折算转动惯量。
分别为Ⅱ、Ⅲ轴转动惯量和工作台质量折算到I轴上的折算转动惯量。
2、粘性阻尼系数的折算
机械系统工作过程中,相互运动的元件间存在着阻力,并以不同的形式表现出来,如摩擦阻力、流体阻力以及负载阻力等,这些阻力在建模时需要折算成与速度有关的粘滞阻尼力。
当工作台均速转动时,轴Ⅲ的驱动转矩T3完全用来克服粘滞阻尼力的消耗。考虑到其它各环节的摩擦损失比工作台导轨的摩擦损失小得多,故只计工作台导轨的粘性阻尼系数C。根据工作台与丝杠之间的动力平衡关系有:
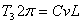
即丝杠转一周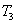 所作的功,等于工作台前进一个导程时其阻尼力所作的功。
所作的功,等于工作台前进一个导程时其阻尼力所作的功。
根据力学原理和传动关系有:
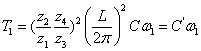 (7)
(7)
式中C′——工作台导轨折算到轴I上的粘性阻力系数
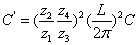 (8)
(8)
12345下一页
