机械系统的制动问题就是讨论在一定时间内把机械装置减速至预定的速度或减速到停止时的相关问题。如机床的工作台停止时的定位精度就取决于制动控制的精度。
制动过程比较复杂,是一个动态过程,为了简化计算,以下近似地作为等减速运动来处理。
1、制动力矩
当已知控制轴的速度(转速)、制动时间、负载力矩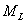 、装置的阻力矩
、装置的阻力矩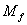 以及等效转动惯量J时,就可计算制动时所需的力矩。因负载力矩也起制动作用,所以也看作制动力矩。下面分析将某一控制轴的转速,在一定时间内由初速
以及等效转动惯量J时,就可计算制动时所需的力矩。因负载力矩也起制动作用,所以也看作制动力矩。下面分析将某一控制轴的转速,在一定时间内由初速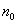 减至预定的转速n的情况。
减至预定的转速n的情况。
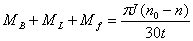
即
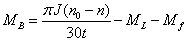 (1)
(1)
式中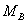 ——控制轴设置的制动力矩(N·m);
——控制轴设置的制动力矩(N·m);
t一制动控制时间(s)。
在式(1)中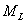 与
与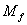 均以其绝对值代入。若已知装置的机械效率
均以其绝对值代入。若已知装置的机械效率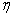 时,则可以通过效率反映阻力矩,既:
时,则可以通过效率反映阻力矩,既: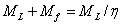 。则上式可写成
。则上式可写成
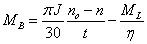 (2)
(2)
2、制动时间
机械装置在制动器选定后,就可计算到停止时所需要的时间。这时,制动力矩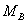 、等效负载力矩
、等效负载力矩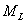 、等效摩擦阻力矩
、等效摩擦阻力矩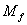 、装置的等效转动惯量J以及制动速度是已知条件。制动开始后,总的制动力矩为
、装置的等效转动惯量J以及制动速度是已知条件。制动开始后,总的制动力矩为
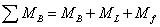 (3)
(3)
由式(1)得
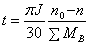 (4)
(4)
3、制动距离(制动转角)
开始制动后,工作台或转臂因其自身惯性作用,往往不是停在预定的位置上。为了提高运动部件停止的位置精度,设计时应确定制动距离以及制动的时间。
设控制轴转速为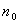 (r/min),直线运动速度为
(r/min),直线运动速度为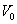 (m/min)。当装在控制轴上的制动器动作后,控制轴减速到n(r/min),工作台速度降到v(m/min),试求减速时间内总的转角和移动距离。
(m/min)。当装在控制轴上的制动器动作后,控制轴减速到n(r/min),工作台速度降到v(m/min),试求减速时间内总的转角和移动距离。
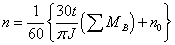
式中,n的单位为r/s。以初速n0(r/min)转动的控制轴上作用有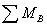 的制动力矩在t秒钟内转了
的制动力矩在t秒钟内转了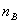 转,
转,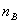 为
为
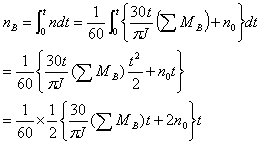
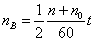 (5)
(5)
将式(4)代入式(5)后得
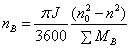 (6)
(6)
由式(6)可求出总回转角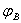 (单位为rad)
(单位为rad)
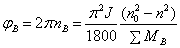 (7)
(7)
用类似的方法可推导有关直线运动的制动距离。设初速度为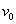 (m/min),终速度为v(m/min),制动时间为t,且认为是匀减速制动,则制动距离
(m/min),终速度为v(m/min),制动时间为t,且认为是匀减速制动,则制动距离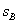 为
为
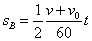 (8)
(8)
当t为未知值时,代人式(3)求得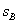 为
为
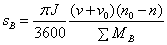 (9)
(9)
