对于步进电机运行的闭环控制,这里采用两输入单输出的模糊控制器。两个输入量分别是天线阵面跟踪角位移的偏差和偏差变化率,输出量是步进电机的运行频率。一个典型的模糊控制器都包含有三个环节:精确量的模糊化、模糊推理和反模糊化。
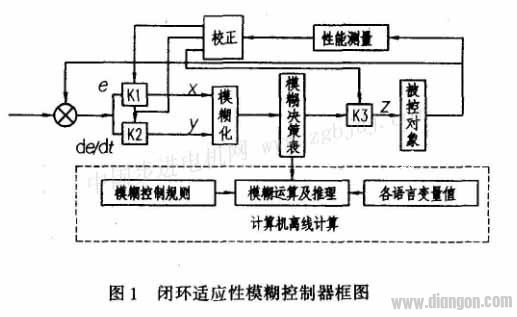
为提高实时性和跟踪精度,这里采用离线模糊推理运算,制定模糊决策表,存入EPRO中,用查表法决定输出量。由于雷达罩天线座测量仪测量参数较多和测量环境的变化(如室外风载荷影响等),在一般场合下,依据原手动断续定点跟踪测量经验总结的知识库则常常具有很大的局限性,致使控制效果受到影响。为此,在反模糊化环节后面,又加入了自适应参数调节环节,以适应不同测量场合和控制过程的突变,提高跟踪效果。因此本文设计的闭环适应性模糊控制器的结构框图如图1所示。
 1.精确量的模糊化
1.精确量的模糊化
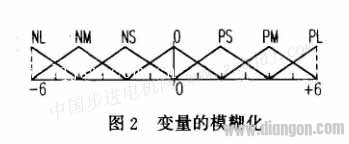
对反馈测量环节得到的方位、俯仰轴的角位移偏差和偏差变化率信号的精确值,首先进行模糊化处理。对于角位移偏差、偏差变化率和控制输出量分别可看作离散整数论域[-6,+6]上的语言变量E、E7和F,并对E、E7、F的语言变量值化分为:PL(正大)、PM(正中)、PS(正小)、O、NS(负小)、NM(负中)、NL(负大)7个档次,其隶属函数取三角分布,如图2所示。
 2.模糊推理及决策表建立
2.模糊推理及决策表建立
模糊推理就是根据一系列语言规则构成的模糊知识库,对输入变量进行推理,而获得控制量的过程,对于图1的模糊控制器结构,这里采取Mamdani推理法,并取如下模糊推理规则:
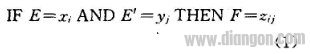
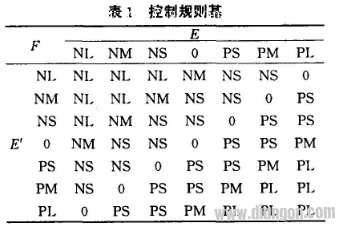
取i=0,1,2,…,7和j=0,1,2,…,7由式(1)产生7×7条控制规则,按照上述对语言变量的值档次的划分,其规则基如表1所示。
根据Mamdani推理法有A×B×C,其对应的模糊关系最为:
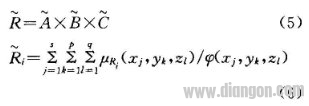
式(2)~(6)中,分别为模糊集合A、B、C、R的隶属度,且:
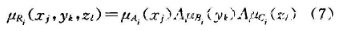
对于已知输入A、B,则输出C可用下式求得:
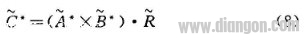 3.模糊量的精确化
3.模糊量的精确化
按上述模糊推理获得的模糊控制量,还需进行精确化处理才能用于实际控制。对模糊量的精确化处理,本文采用工业控制中广泛应用的加权平均法:
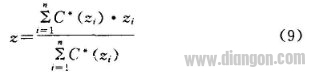
按照上述推理,离线计算得出模糊决策表,存人计算机内存,在跟踪控制过程中靠查表法迅速得出控制量,从而大大提高了实时跟踪能力和跟踪精度。
4.量化因子的适应性调节
由于雷达罩天线座跟踪测量仪测量参数较多,且既有静态测量又有动态测量,而上述决策表模糊推理知识库是在一个方向为零角度(零点位置)而另一方向上为-60度~+60度全行程范围内手动跟踪测量得出的经验总结,在其它场合下的参数测量时,模糊控制效果则不一定好,因此为使跟踪效果更好,在基本模糊控制器的基础上,又增加了输入、输出量化因子的适应性调节环节,以更好地适应各测量场合。
当偏差e或偏差变化率△P较大时,缩小K
1、K
2降低大偏差范围内的分辨率,以获得较平缓的控制特性,保证系统的稳定性;同时增大K
3提高快速性,改善系统的动态性能。
当偏差e或偏差变化率△P较小时,系统已接近稳态,则调节增大K
1、K
2,提高系统对小偏差的分辨率,提高控制的灵敏度;同时缩小K
3,以避免超调和振荡,使系统尽快进入稳态精度范围内。量化因子K
1、K
2、K
3的调节规律如图3所示。
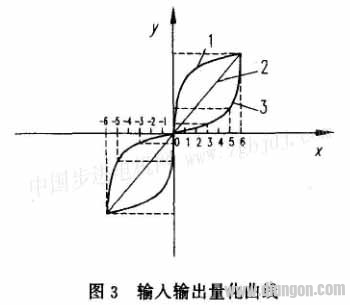
图3中,1为两个输入量的量化曲线,其上各点的斜率为量化因子K
1、K
2的适应性调节规律,2为调节的恒定量化因子,3为输出量的量化曲线,其各点的斜率为K3的适应性调节规律。
提醒:《步进伺服系统适应性模糊控制器设计》最后刷新时间 2023-07-10 04:11:07,本站为公益型个人网站,仅供个人学习和记录信息,不进行任何商业性质的盈利。如果内容、图片资源失效或内容涉及侵权,请反馈至,我们会及时处理。本站只保证内容的可读性,无法保证真实性,《步进伺服系统适应性模糊控制器设计》该内容的真实性请自行鉴别。
 1.精确量的模糊化
对反馈测量环节得到的方位、俯仰轴的角位移偏差和偏差变化率信号的精确值,首先进行模糊化处理。对于角位移偏差、偏差变化率和控制输出量分别可看作离散整数论域[-6,+6]上的语言变量E、E7和F,并对E、E7、F的语言变量值化分为:PL(正大)、PM(正中)、PS(正小)、O、NS(负小)、NM(负中)、NL(负大)7个档次,其隶属函数取三角分布,如图2所示。
1.精确量的模糊化
对反馈测量环节得到的方位、俯仰轴的角位移偏差和偏差变化率信号的精确值,首先进行模糊化处理。对于角位移偏差、偏差变化率和控制输出量分别可看作离散整数论域[-6,+6]上的语言变量E、E7和F,并对E、E7、F的语言变量值化分为:PL(正大)、PM(正中)、PS(正小)、O、NS(负小)、NM(负中)、NL(负大)7个档次,其隶属函数取三角分布,如图2所示。
 2.模糊推理及决策表建立
模糊推理就是根据一系列语言规则构成的模糊知识库,对输入变量进行推理,而获得控制量的过程,对于图1的模糊控制器结构,这里采取Mamdani推理法,并取如下模糊推理规则:
2.模糊推理及决策表建立
模糊推理就是根据一系列语言规则构成的模糊知识库,对输入变量进行推理,而获得控制量的过程,对于图1的模糊控制器结构,这里采取Mamdani推理法,并取如下模糊推理规则:
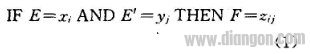 取i=0,1,2,…,7和j=0,1,2,…,7由式(1)产生7×7条控制规则,按照上述对语言变量的值档次的划分,其规则基如表1所示。
取i=0,1,2,…,7和j=0,1,2,…,7由式(1)产生7×7条控制规则,按照上述对语言变量的值档次的划分,其规则基如表1所示。
 根据Mamdani推理法有A×B×C,其对应的模糊关系最为:
根据Mamdani推理法有A×B×C,其对应的模糊关系最为:
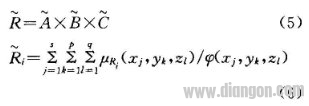 式(2)~(6)中,分别为模糊集合A、B、C、R的隶属度,且:
式(2)~(6)中,分别为模糊集合A、B、C、R的隶属度,且:
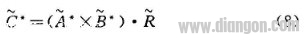 3.模糊量的精确化
按上述模糊推理获得的模糊控制量,还需进行精确化处理才能用于实际控制。对模糊量的精确化处理,本文采用工业控制中广泛应用的加权平均法:
3.模糊量的精确化
按上述模糊推理获得的模糊控制量,还需进行精确化处理才能用于实际控制。对模糊量的精确化处理,本文采用工业控制中广泛应用的加权平均法:
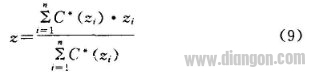 按照上述推理,离线计算得出模糊决策表,存人计算机内存,在跟踪控制过程中靠查表法迅速得出控制量,从而大大提高了实时跟踪能力和跟踪精度。
4.量化因子的适应性调节
由于雷达罩天线座跟踪测量仪测量参数较多,且既有静态测量又有动态测量,而上述决策表模糊推理知识库是在一个方向为零角度(零点位置)而另一方向上为-60度~+60度全行程范围内手动跟踪测量得出的经验总结,在其它场合下的参数测量时,模糊控制效果则不一定好,因此为使跟踪效果更好,在基本模糊控制器的基础上,又增加了输入、输出量化因子的适应性调节环节,以更好地适应各测量场合。
当偏差e或偏差变化率△P较大时,缩小K1、K2降低大偏差范围内的分辨率,以获得较平缓的控制特性,保证系统的稳定性;同时增大K3提高快速性,改善系统的动态性能。
当偏差e或偏差变化率△P较小时,系统已接近稳态,则调节增大K1、K2,提高系统对小偏差的分辨率,提高控制的灵敏度;同时缩小K3,以避免超调和振荡,使系统尽快进入稳态精度范围内。量化因子K1、K2、K3的调节规律如图3所示。
按照上述推理,离线计算得出模糊决策表,存人计算机内存,在跟踪控制过程中靠查表法迅速得出控制量,从而大大提高了实时跟踪能力和跟踪精度。
4.量化因子的适应性调节
由于雷达罩天线座跟踪测量仪测量参数较多,且既有静态测量又有动态测量,而上述决策表模糊推理知识库是在一个方向为零角度(零点位置)而另一方向上为-60度~+60度全行程范围内手动跟踪测量得出的经验总结,在其它场合下的参数测量时,模糊控制效果则不一定好,因此为使跟踪效果更好,在基本模糊控制器的基础上,又增加了输入、输出量化因子的适应性调节环节,以更好地适应各测量场合。
当偏差e或偏差变化率△P较大时,缩小K1、K2降低大偏差范围内的分辨率,以获得较平缓的控制特性,保证系统的稳定性;同时增大K3提高快速性,改善系统的动态性能。
当偏差e或偏差变化率△P较小时,系统已接近稳态,则调节增大K1、K2,提高系统对小偏差的分辨率,提高控制的灵敏度;同时缩小K3,以避免超调和振荡,使系统尽快进入稳态精度范围内。量化因子K1、K2、K3的调节规律如图3所示。
 图3中,1为两个输入量的量化曲线,其上各点的斜率为量化因子K1、K2的适应性调节规律,2为调节的恒定量化因子,3为输出量的量化曲线,其各点的斜率为K3的适应性调节规律。
图3中,1为两个输入量的量化曲线,其上各点的斜率为量化因子K1、K2的适应性调节规律,2为调节的恒定量化因子,3为输出量的量化曲线,其各点的斜率为K3的适应性调节规律。
