设计一个自动调节系统首先保证它的稳定性,并且使系统有足够大的稳定储各,即在对数频率特性图( Bode图)上表现出有足够的稳定裕量,包括增益裕量和相位裕量,其定义可以在系统的开环频率特性上了 解,如图所示。
增益裕量
式中 ω1——相频特性曲线穿越-180°时的频率,称为相位交越频率。
以分贝数表示的K>0时,系统是稳定的。
相位裕量为
式中 ωc——幅频特性曲线穿越0 dB时的频率,称为增益交越频率或穿越频率,由|G(jωc)|=1
求得。
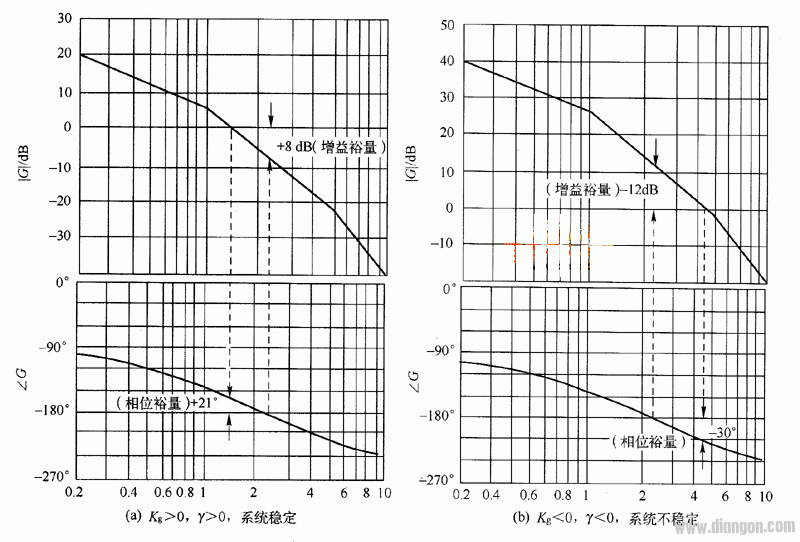
图 对数频率特性
γ与阻尼ζ相关,对干二阶闭环系统,不同ζ的相应γ计算值如表
表 二阶闭环系统相位裕量γ与阻尼比ζ计算值
当ζ=0时,相频特性正好在ωc处穿越-180°,即ωc=ω1,则γ=0。即稳定裕量为零,这时的时域响应为等幅振荡。图1(b)中,γ<0,Kg<0系统是不稳定的。
一般要求所设计的系统,增益裕量应大于6dB,相位裕量为30°~60°。如果稳定裕量过小,则系统阶跃响应的振荡次数较多,超调量较大;如果稳定裕量过大,则系统响应太慢,调节时间较长。
