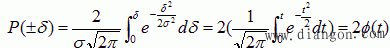1.置信概率与置信区间
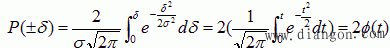置信区间 ：即所选择的这个范围，一般用标准差的倍数表示，如
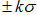
；置信度（置信概率）：用来描述测量结果处于某一范围内（
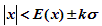
）内包含真值的可靠程度的量，一般用百分数表示。 
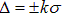
k——置信系数（或置信因子）
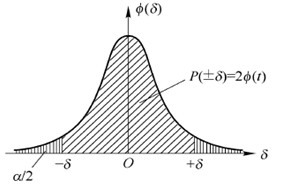图2-14 置信概率与置信区间
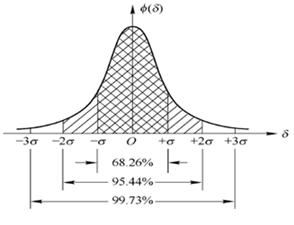图2-15 正态分布的置信概率与置信区间
当分布和k值确定之后，则置信概率可定 ，
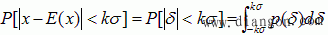
正态分布,当k=3时，
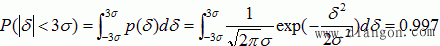
，如图2-15所示，对于同一个测量结果来说，所取置信区间愈宽，则置信概率愈大，反之愈小。正态分布的随机误差，其绝对值小于3σ的概率为99.7%，因此定义∆=3σ为极限误差。 2.有限次测量时的置信问题（略）
二、不确定度与坏值的剔除准则
剔除是要有一定依据的。在不明原因的情况下，首先要判断可疑数据是否是粗大误差。其方法的基本思想是给定一置信概率，确定相应的置信区间，凡超出置信区间的误差就认为是粗大误差。
一般情况，正态分布比较多，也就是k=3时，即在以3倍标准差±3σ区间内，随机误差出现的概率为99.73%，而在这个区间外的概率非常小。
根据上述理由，在测量数据中，如果出现大于 3σ的误差，则可认为该次测量值是坏值，应予剔除，即
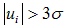
，通常采用的3σ准则。