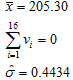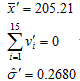1．有效数字
由于含有误差，所以测量数据及由测量数据计算出来的算术平均值等都是近似值。
（1）若末位数字是个位，则包含的绝对误差值不大于0.5；
（2）若末位是十位，则包含的绝对误差值不大于5；
（3）对于其绝对误差不大于末位数字一半的数，从它左边第一个不为零的数字起，到右面最后一个数字(包括零)止，都叫做有效数字。中间的0和末尾的0都是有效数字，不能随意添加。开头的零不是有效数字。
测量数据的绝对值比较大（或比较小），而有效数字又比较少的测量数据，应采用科学计数法，即a×10n，a的位数由有效数字的位数所决定。
例1 用10v指针式电压表测得 U= 5. 6 4 V 三位有效数字 ，如图1：
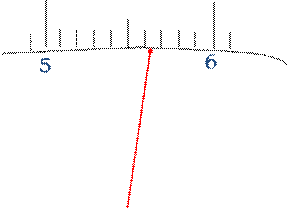
图1 有效数字示意图
最末位有效数字常称存疑数，它主要由仪表所能达到的精度决定。例如用10V量程指针式电压表测得电压5.64V，这是三位有效数字组成的数据，这三位数中前二位是可从刻度上准确读出的，而最后一位是估读的，是含有误差的近似数，常称为存疑数。
例2 0.0038KΩ=3.8Ω ，两位有效数字；
例3 0.026m 两位有效数字，
0.0260m 三位有效数字；
例4 8700 四位有效数字，
87×102 两位有效数字；
2.多余数字的舍入规则
由于测量数据和测量结果均是近似数，其位数各不相同。为了使测量结果的表示准确唯一，计算简便，在数据处理时，需对测量数据和所用常数进行修约处理。
数据修约规则：
（1） 小于5舍去——末位不变。
（2） 大于5进1——在末位增1。
（3） 等于5时，取偶数——当末位是偶数，末位不变；末位是奇数，在末位增1（将末位凑为偶数）
例5 ：将下列数字保留到小数点后一位：l2.34，l2.36，l2.35，l2.45。
解： 12.34 →l2.3 (4<5，舍去)
12.36→l2.4 (6>5， 进一)
l2.35 → l2.4 (3是奇数，5入)
12.45→ 12.4 (4是偶数，5舍)
例6： 将下列数据舍入到小数第二位。
12.4344→12.43 63.73501→63.74
0.69499→0.69 25.3250→25.32 17.6955→17.70 123.1150→123.12
需要注意的是，舍入应一次到位，不能逐位舍入。
二、 等精密度测量结果的处理步骤
①用修正值等方法，减小恒值系统误差的影响, 列出测量数据x1，x2，x3，……，xn。
②求算术平均值, 
;
③求剩余误差（残差）vi=xi–
，并验证。
④用贝塞尔公式计算标准偏差估计值：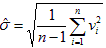
;
⑤利用莱特准则，即3σ准则，判别是否存在粗差。
⑥剔除坏值后，再重复求剩下数据的算术平均值、剩余误差及标准差，并再次判断，直至不包括坏值为止。
⑦判断有无变值系统误差。
⑧求算术平均值的标准差估计值
⑨求算术平均值的不确定度
⑩给出测量结果的表达式（报告值）
。
例7：对某电压进行了16次等精密度测量，测量数据中已计入修正值，列于表1–1要求给出包括误差（即不确定度）在内的测量结果表达式。
表1–1 测量值及其计算值 | ||||||
|
n |
xi/V |
首次计算 |
第二次计算 |
|||
|
vi |
vi2 |
vi′ |
(vi′)2 |
备注 | ||
|
1 |
205.24 |
－0.06 |
0.0036 |
＋0.03 |
0.0009 |
|
|
2 |
205.21 |
－0.09 |
0.0081 |
0.00 |
0.0000 |
|
|
3 |
205.35 |
＋0.05 |
0.0025 |
＋0.14 |
0.0196 |
|
|
4 |
204.94 |
－0.36 |
0.1296 |
－0.27 |
0.0729 |
|
|
5 |
205.32 |
＋0.02 |
0.0004 |
＋0.11 |
0.0121 |
|
|
6 |
204.97 |
－0.33 |
0.1089 |
－0.24 |
0.0576 |
|
|
7 |
205.71 |
＋0.41 |
0.1681 |
＋0.50 |
0.2500 |
|
|
8 |
205.63 |
＋0.33 |
0.1089 |
＋0.42 |
0.1764 |
|
|
9 |
204.70 |
－0.60 |
0.3600 |
－0.51 |
0.2601 |
|
|
10 |
205.30 |
＋0.00 |
0.0000 |
＋0.09 |
0.0081 |
|
|
11 |
205.36 |
＋0.06 |
0.0036 |
＋0.15 |
0.0225 |
|
|
12 |
205.21 |
－0.09 |
0.0081 |
0.00 |
0.0000 |
|
|
13 |
204.86 |
－0.44 |
0.1936 |
－0.35 |
0.1225 |
|
|
14 |
206.65 |
＋1.35 |
1.8225 |
x13为坏值 | ||
|
15 |
205.19 |
－0.11 |
0.0121 |
－0.02 |
0.0004 |
|
|
16 |
205.16 |
－0.14 |
0.0196 |
－0.05 |
0.0025 |
|
|
计算值 |
|
|
||||
解：①求出算术平均值：
；
②计算残差vi列于表中，并验证
；
③计算标准差(估计值)：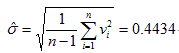 
④利用莱特准则判别是否存在粗差。查表中第14个数据的残差v14=1.35>3
=1.33，应将此对应的x14=206.65视为坏值加以剔除，现剩下15个数据；
⑤重新计算剩余15个数据的平均值：
；
⑥重新计算残差vi′，列于表中，并验证
；
⑦重新计算标准差(估计值)：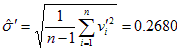 
⑧再利用莱特准则判别是否存在粗差。现各残差vi′<3
=0.804，则认为剩余数据中不再含有坏值，并且n=15>10；
⑨对vi′作图，判断有无变值系差，见图2，从图中可见无明显累进性或周期性系差；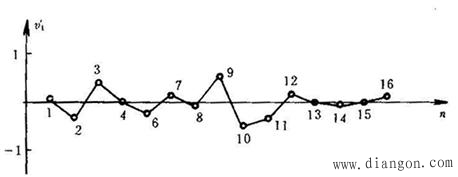 
图2 计算举例中vi′的变化情况
⑩计算算术平均值标准偏差(估计值)： 
⑪写出测量结果表达式： 
此外，曲线修匀，最小二乘法原理，测量不确定度这里从略，具体参见教材，这些部分为了解内容。