| 三相输电线路通以交流电流时,导体周围产生电磁场,该电磁场沿线做均匀分布,电磁能转变为热能也是沿全线进行的,故三相输电线路是一分布参数的电路。三相输电线路正常运行时,三相电压、电流处于对称情况,分析时就以其中一相即可。输电线路的单相等值电路为 |
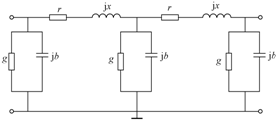 |
| 图1电力线路的单相等值电路 |
| 用图1所示的分布参数等值电路进行输电线的电气计算是比较复杂的,为了简化计算,工程上一般根据线路的长短采用以下几种等值电路。 1.短电力线路的一字形等值电路 对于线路长度不超过100km的短架空线路和不长的电缆线路,称短电力线路;当电压不高时线路电纳及电导可忽略不计。这样就得到了只有电阻和电抗两个参数表示的一字形等值电路,Z=R+jX,如图2所示。 |
 |
| 图2一字型等值电路 图3双端口网络 |
| 由图可得 |
| |
| 将式(2-37)与电路理论课程中介绍的双端口网络方程式相比较, 双端口网络如图3所示, |
| |
| 可得这种等值电路的通用常数A、B、C、D ,其中A=1,B=Z,C=0,D=1。 传输参数矩阵: |
| |
| 2.中等长度线路的П型和Τ型等值电路 电力线路的模型,是一个分布参数的电路。以架空线路为重点,要能分析各种因素(例如天气)对架空线路参数的影响,并根据导线标号、它们在杆塔的布置和线路长度,计算线路的阻抗、导纳、电晕、临界电压等参数,来建立等值电路模型。 对于长度在100-300km的架空线路或不超过100km的电缆线路,称中等长度电力线路,其电纳的影响已不能忽略,故通常采用П型和Τ型等值电路。如图4所示,其中,常用的是∏型等值电路。 |
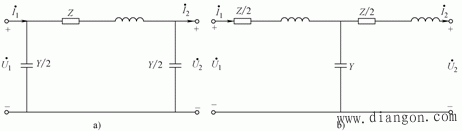 |
| (a)П型等值电路 (b)Τ型等值电路 图4中等长度线路等值电路 |
| 在П型等值电路中,除串联的线路总阻抗Z=R+jX之外,还将线路的总导纳Y=jB分为两半,分别并联在线路的始末端。在Τ型等值电路中,线路的总导纳集中在中间,而线路的总阻抗则分为两半,分别串联在它的两侧。因此,这两种电路都是近似的等值电路,而且,相互间并不等值,即它们不能用△-Y变换公式相互变换。 由图4可得流过串联阻抗Z的电流为 |
| |
| 从而得到始端电压电流与末端电压电流的关系为 |
| |
| 写成矩阵形式为 |
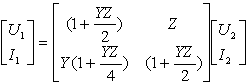 (5) (5) |
| 将式(2-41)与式(2-39)相比较,可得这种等值电路的通用常数 |
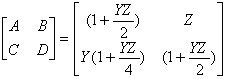 |
| 类似地,可得Τ型等值电路中的通用常数 |
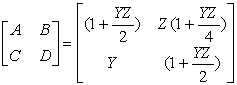 |
| 若已知A、B、C、D参数,也可由以上公式推导出П型等值电路各参数与传输参数的关系: |
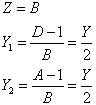 |
| 上述计算得到的参数与图(4)中П型等值电路参数一致。 例(1) 某110kV架空线路全长100km,导线水平排列,相间距离为4m,导线型号为LGJ-240,导线半径为r=10.8mm。试计算线路的电气参数,并作出П型等值电路。 解: 每公里线路电阻的计算: r=ρ/S=31.5/240=0.1313(Ω/km) 每公里电抗计算 导线水平排列时的几何均距为: Dm=1.26D=1.26*4000=5040(mm) 电抗: |
| |
| 电纳: |
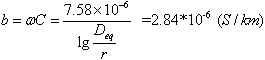 |
| 全线路参数为: R=rl=0.1313*100=13.13(Ω) X=xl=0.401*100=40.1(Ω) B=bl=2.84*10-6*100=2.84*10-4(S) B/2=j1.42*10-4 |
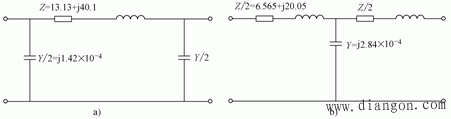 |
| (a)П型等值电路 (b)Τ型等值电路 图5 例1 线路等值电路 |
| 3.远距离输电线路的等值电路 若线路是长度超过300km的架空线路和超过100km的电缆线路,属于远距离输电线路,这种线路等值电路也可采用П型或Τ型等值电路。 |
| |
| 远距离输电线路的П型或Τ型等值电路如图6所示,实际应用时大多采用П型等值电路, |
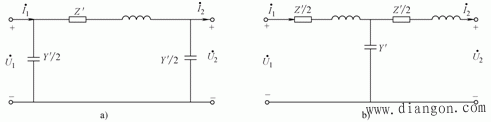 |
| (a)П型等值电路 (b)Τ型等值电路 图6 线路等值电路 |
| 根据上述的A、B、C、D参数,可推导出远距离输电线路П型等值电路中的各参数与传输参数的关系, |
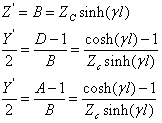 |
| 对于远距离输电线路,若不考虑其分布参数,将给计算结果带来较大的误差,电阻误差大于10%,电抗次之,电纳更次之。 |
导读:目前正在解读《电力线路的数学模型》的相关信息,《电力线路的数学模型》是由用户自行发布的知识型内容!下面请观看由(电工学习网 - www.9pbb.com)用户发布《电力线路的数学模型》的详细说明。
提醒:《电力线路的数学模型》最后刷新时间 2023-07-10 04:01:42,本站为公益型个人网站,仅供个人学习和记录信息,不进行任何商业性质的盈利。如果内容、图片资源失效或内容涉及侵权,请反馈至,我们会及时处理。本站只保证内容的可读性,无法保证真实性,《电力线路的数学模型》该内容的真实性请自行鉴别。
