逻辑代数的基本运算有哪三种?

逻辑代数是按照一定的逻辑规则进行逻辑运算的代数，是分析数字电路的数学工具。对应于逻辑与、逻辑或和逻辑非三种基本逻辑关系，逻辑代数的基本逻辑运算有三种：逻辑乘、逻辑加和逻辑非。
一、逻辑变量有什么特点
逻辑代数中的变量，包括自变量（前因）和因变量（后果），都只有两个取值：“1”和“0”。在逻辑代数中，“1”和“0”不表示具体的数量，而只是表示逻辑状态。例如，电位的高与低、信号的有与无、电路的通与断、开关的闭合与断开、晶体管的截止与导通，等等。
二、逻辑乘
反映逻辑与关系的逻辑运算叫做逻辑乘，其逻辑函数表达
式为：

Y=A·B（可简写为：Y=AB）

式中，A和B是输入变量，Y是输出变量，“· ”表示逻辑乘运算。
1．逻辑乘的意义
逻辑乘的意义是：A和B都为“1”时，Y才为“1”；A 和B中只要有一个为“0”时，Y必为“0”。
例如，在上节提到的两个开关串联控制电灯的电路中（见图2-2），设开关闭合为“1”、断开为“0”，电灯亮为“1”、不亮为“0”，则很明显可以看出：只有当A(S₁) = 1并且B(S₂) = 1时，才有Y(EL) = 1；A和B中只要有一个为0时，则Y(EL) = 0。由此可见，逻辑乘的运算规则为：
0·0 = 0
0·1 = 0
1·0 = 0
1·1 = 1
将以上运算规则列表，即为逻辑乘的逻辑函数真值表，如表2-4所示。

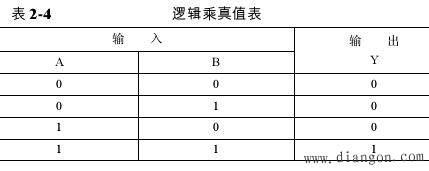
2．逻辑乘的实现电路
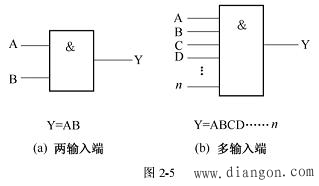
实现逻辑乘的数字电路是与门。图2-5（a）所示为A、B两个输入端的与门，可实现A、B两个输入变量的逻辑乘运算。
逻辑乘的输入变量可以有两个以上，分别用A、B、C、D.表示，相应的逻辑函数表达式为：Y=ABCD.图2-5（b）所示为多输入端与门。

三、逻辑加
反映逻辑或关系的逻辑运算叫做逻辑加，其逻辑函数表达式为：

Y=A+B

式中，A和B是输入变量，Y是输出变量，“+”表示逻辑加运算。
1．逻辑加的意义
逻辑加的意义是：A和B中只要有一个或一个以上为“1”时，Y即为“1”；只有A和B都为“0”时，Y才为“0”。
例如，在上节提到的两个开关并联控制电灯的电路中（见图2-3），设开关闭合为“1”、断开为“0”，电灯亮为“1”、不亮为“0”，则很明显可以看出：只要当A(S₁) =1，或者B(S₂) =1，或者A、B都=1时，就有Y(EL) =1；只有A和B都为0时，才有Y(EL) = 0。由此可见，逻辑加的运算规则为：

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 1

将以上运算规则列表，即为逻辑加的逻辑函数真值表，如表2-5 所示。
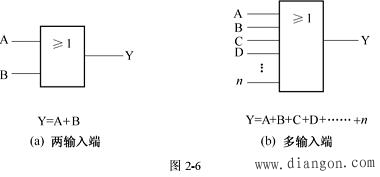
2．逻辑加的实现电路
实现逻辑加的数字电路是或门。图2-6（a）所示为A、B两个输入端的或门，可实现A、B两个输入变量的逻辑加运算。逻辑加的输入变量可以有两个以上，分别用A、B、C、D.表示，相应的逻辑函数表达式为：Y=A+B+C+D+.图2-6（b）所示为多输入端或门。

四、逻辑非
反映逻辑非关系的逻辑运算仍叫做逻辑非，其逻辑函数表达式为：

Y=

式中，A是输入变量，Y是输出变量，“A”上面加一杠（）表示对变量A进行逻辑非运算。
1．逻辑非的意义
逻辑非的意义是：A为“1”时，Y即为“0”；A为“0”时，Y即为“1”；Y总是与A相反。
例如，在上节提到的旁路开关控制电灯的电路中（见图2-4），设开关闭合为“1”、断开为“0”，电灯亮为“1”、不亮为“0”，则很明显可以看出：当A(S)=1时，Y(EL) = 0；当A(S)=0时，Y(EL) =1。由此可见，逻辑非的运算规则为：

将以上运算规则列表，即为逻辑非的逻辑函数真值表，如表2-6 所示。

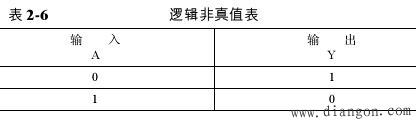
2．逻辑非的实现电路
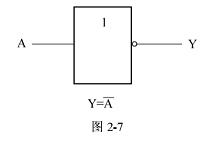
实现逻辑非的数字电路是非门，也称为反相器。图2-7所示为非门，A为输入端，Y为输出端。

五、基本公式和定律
在分析和解读数字电路时，需要用到一些逻辑代数的基本公式和基本定律。这些基本公式和定律，有的与普通代数相似，例如交换律、结合律、分配律等；有的则是逻辑代数所特有的，例如0-1律、重叠律、互补律、还原律、摩根定理等。下面着重介绍逻辑代数的特殊公式和定律。
1．0-1律
0-1律是逻辑代数的基本定律之一，可用以下4个公式表述：

0·A = 0　　　　　（1）

1·A = A 　　　　　（2）

0 + A = A 　　　　　（3）

1 + A = 1 　　　　　（4）

以上公式很好理解。前两式属于逻辑乘运算，只有1·1 = 1，否则结果都等于0，因此，（1）式的结果恒等于0，（2）式的结果由A决定。后两式属于逻辑加运算，加数中只要有1，结果就为1，因此，（3）式的结果由A决定，（4）式的结果恒等于1。
2．重叠律
重叠律可用以下2个公式表述：

A + A = A 　　　　　（5）

A·A = A 　　　　　（6）

因为A是逻辑变量，取值只能是0或1。在逻辑加运算中，0 + 0 = 0，1 + 1 = 1，所以（5）式成立。在逻辑乘运算中，0· 0 = 0，1·1 = 1，所以（6）式成立。
3．互补律
互补律可用公式（7）和公式（8）表述：

A += 1 　　　　　（7）

A·= 0　　　　　 （8）

因为A和中必定一个是1、另一个是0，（7）式是逻辑加运算，1 + 0 = 1；（8）式是逻辑乘运算，1·0 = 0。
4．还原律
还原律可用公式（9）表述：

由于逻辑变量只有1和0两个状态，（9）式说明当对一个逻辑变量进行两次反相后，必然等于该逻辑变量本身。
5．摩根定理
摩根定理可用公式（10）和公式（11）表述：

摩根定理又叫反演律，它将逻辑加与逻辑乘有机联系在一起，实现了两者的互相转换，给我们研究、分析和设计数字逻辑电路提供了极大的方便。摩根定理是逻辑代数中最重要的定理之一。
当有两个以上的逻辑变量时，摩根定理仍然成立，即

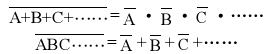
摩根定理可以用列逻辑函数真值表的方法予以证明。
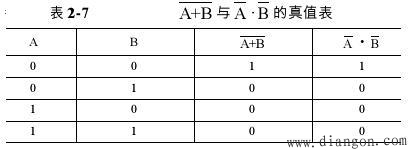
（1）表2-7所示为与·的真值表，从表中可以看到与·的状态完全相同，因此=·，（10）式成立。

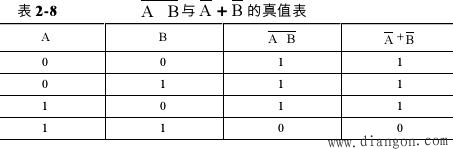
（2）表2-8所示为与+的真值表，同样证明了=+，（11）式成立。