输电线路导线的振动和防振

在气象条件三要素（风速、覆冰厚度和气温）中，风的作用除产生了作用于导线和杆塔的垂直线路方向的水平荷载外，也是导线发生振动的根本原因。导线的振动将使导线产生断股、断线或引起相间闪络，造成线路跳闸停电等事故，严重危及输电线路的正常运行，所以在设计时必须考虑导线振动问题。 一、导线的振动和防振 　　（一）振动的起因
　　架空输电线路的导线（避雷线）受到稳定的微风作用时，便在导线背后形成以一定频率上下交替变化的气流旋涡，如图（1）所示，从而使导线受到一个上下交变的脉冲力作用。 　　　
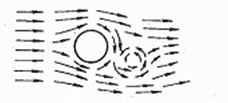
　　　图1　引起导线振动的气流旋涡
　　当气流旋涡的交替变化频率与导线的固有自振频率相等时，将使导线在垂直平面内产生共振即引起导线振动。
　　导线振动的波形为驻波，即波节不变，波腹上下交替变化，而且一年中导线振动的时间常达全年时间30%－50%。无论导线以什么频率振动，在其线夹出口处总是一波节点，所以，导线振动使导线在线夹出口处会反复拗折，引起材料疲劳，最后导致断股、断线事故、对线路的正常安全运行危害较大。
　　（二）导线振动的特性和影响因素
　　1．导线振动的特性
　　　了解波运动首先应明确以下的有关参数：
　　　　1）振幅—波离开水平位置的距离，m；
　　　　2）波长—振动波在一个周期内所行进的长度，m；
　　　　3）频率—单位周期内（波长）所变化的次数Hz。
　　（1）振动波形、振幅和振动角。
　　导线的振动是沿整档导线呈驻波分布的，即导线离开平衡位置的位移大小无论在时间上还是沿档距长度上都是按正弦规律变化的，同时在同一频率下，波腹点Am（最大振幅）及波节（即半波长的整数倍）在导线上的位置恒定不变。图2为某一频率时导线振动的波形示意图。
　　　
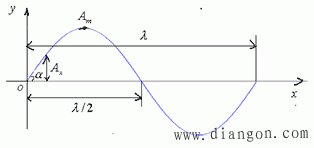
　　　　　　　　　图2 导线振动的波形
　　其中,坐标原点为波节点，导线离开平衡位置OX 轴距离AX称为振幅。位移中最大者Am称为最大振幅。
　　统计观察表明，导线的振幅与导线应力的大小有关，当导线应力为导线破坏应力的8%时，振幅接近于零；当导线应力增加到导线破坏应力的10%－15%时，振幅迅速增大；当导线应力增加到导线破坏应力的的20%以后，振幅趋于饱和而变化很小。
　　振幅的大小还与空气气流对导线的冲击形式和气流能量的大小有关，并与导线各股间的磨擦有关，波腹点的振幅与波长有关，且在相当于低频率振动又是最大波长时的振幅最大。实际中，振幅一般不超过导线的直径，最大振幅也不会超过导线直径的2－3倍。
　　在评价线夹出口处导线振动弯曲程度时，则常以线夹出口处振动角来表示更为直观。
　　所谓振动角是指导线振动波的波节点处，导线对中心平衡位置的夹角，如图2中的α。显然α是振动波在节点处的斜率角，且最大振幅时振动角也最大。如果在运行中测得距线夹出口处为x点的振幅为Ax，则可按下式求得最大振动角;α_m为
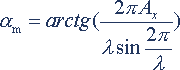　　　　　（1）
　　　式中　α_m—最大振动角；
　　　　　　λ—振动波波长，m；
　　　　　　x —测量点与线夹出口处的距离，m；
　　　　　　A_x—测量点振动波的振幅，m。
　　通常在运行的线路上，导线的振动一般在30′－50′之间，当振动特别强烈时，则接近1°。这样大的振动角，不需要很长时间就会使导线断股，因此一般架空输电线路均需采取防振措施，且在导线紧线后应尽快安装防振器具，以使导线的振动角减小到允许范围内。
　　导线的允许振动角如表3―1所示，这是衡量振动的严重程度和评价防振装置的防振效果的标准。
　　表3-1 导线的允许振动角

平均运行应力	允许振动角（’）
≤25％σp	10
＞25％σp	5

　　（2）导线振动的频率和波长。
　　引起导线振动的原因是气流旋涡的交替变化频率与导线的固有自振频率相等而发生共振。
　　根据试验，当导线受到稳定的微风作用时，气流旋涡的交替变化频率与风速和导线直径有关，其频率可由下式确定
　　　　　（3－8）
　　　式中　f_F—气流旋涡的交替变化频率，HZ；
　　　　　　v—风速，m/s；
　　　　　　d—导线直径，mm。
　　一个物体在振动过程中，如果没有能够影响它振动的力去干扰它，那么，它振动的振幅将保持不变，并只在回复力的作用下永远继续下去，这样的振动叫自由振动（未强迫）。物体作自由振动的频率叫做物体的固有自振频率，固有自振频率是由组成物体的系统本身决定的，输电线路的导线可以看成是两端固定的一条弦线。有关弦振动的自由振动方程推导略，导线的固有自振频率可以下式表示：
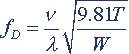　　　　　　（3）
　　　或
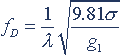　　　　　　（4）
　　式中　f_D—导线的固有自振频率，Hz；
　　　　　T—导线的张力，N；
　　　　　W—导线的单位长度重力，N/m；
　　　　　σ—导线的应力，Mpa；
　　　　　g₁—导线的自重比载，N/ m·mm²。
　　 导线的振动是气流旋涡引起的上下交变的冲力作用下维持的振动，因此是一种受迫振动，物体作受迫振动时，其振动频率总是等于策动力的频率，它的振幅与其固有自振频率和策动力的频率有关，当物体的固有自振频率和策动力的频率相等时，其振动的振幅最大，这种现象称为共振。我们说的导线振动，就是指导线固有自振频率和气流旋涡的交替变化频率相等时的振动，即f_D＝f_F。
　　 由f_D和f_F计算式可知，导线固有自振频率f_D和导线应力σ有关，随着应力的变化，导线有不同的固有自振频率。而气流旋涡的交替变化频率f_F与风速V有关。因此，当气流旋涡的交替变化频率f_F与导线某一固有自振频率f_D相等时，导线在该频率下产生共振，此时振幅达到最大值。当风速变化致使 变化时，振幅将有所下降，同时导线应力也有所变化，导线固有频率也随之变化。
　　此时有可能在另一频率下又实现f_D＝f_F，产生新的共振。因此振动的频率不是惟一的。
　　根据共振的条件f_D＝f_F则可以求出导线振动波的波长为
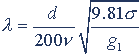　　　　　（5）
　　振动波的半波长为
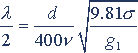　　　　　（6）
　　2．影响振动的因素
　　影响振动的因素主要有：风速、风向、档距、悬点高度、导线应力以及地形、地物等。
　　(1)风的影响。引起振动的基本因素是均匀稳定的微风。因为一方面导线振动的产生和维持需要一定的能量（克服空气阻力、导线股线间的磨擦力等所需的最小能量），而这些能量需由气流旋涡对导线的冲击能量转化而来。
　　一般产生导线振动的最小风速取0.5－0.8m/s,风速再小就不会发生振动。另一方面，维持导线的持续振动，则其振动频率必须相对稳定，也即要求风速应具有一定的均匀性，如果风速不规则地大幅度变化，则导线不可能形成持续的振动，甚至不发生振动。影响风速均匀性的因素有风速的大小，导线悬挂高度、档距、风向和地貌等。
　　当风速较大时，由于和地面摩擦加剧，使地面以上一定高度范围内的风速均匀性遭到破坏。如果档距增大，则为保证导线对地距离，导线悬挂点必然增高。离地面越高，风速受地貌的影响越小，均匀性越好。所以必须适当选择引起导线振动的风速范围，有关防振设计中所取风速数值见书中介绍。
　　由此得出结论：
　　当风速小于0.5－0.8m/s时，虽然可形成均匀稳定气流，但它给予导线的能量小而不足以使导线振动，此称为下限风速。反之，风速过大时，由于不能形成均匀稳定气流其导线振动条件破坏，也不会使导线振动。将导线产生振动的最大风速称为上限风速，其值约5m/s左右。
　　根据在平原开阔地区的观察结果表明，当风向和线路方向成45°～90°夹角时，导线易产生稳定振动；在30°～45°时，振动的稳定性较小；夹角小于20°时，则很少出现振动。
　　因此，引起导线振动既与风速有关，也与风向有关。风速过大不易形成均匀稳定气流，风速过小其能量较小，则均不能使导线振动，而风向影响着导线的振动是否稳定性问题。
　　(2)导线的直径和档距的影响。由波长计算式(3-12)可知，振动波的波长和导线直径有关；另一方面在振动过程中，档距L中振动波的半波数n应为整数，即
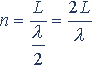
　　则
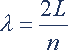
　　将上式代入式(3-12)可得
　　即当风速和导线应力不变时有
　　由上式可知，档距越大、导线直径越小，档中形成完整半波数的机会越多，也就是导线产生共振的机会越多，导线共振程度也越严重。实际观测证实，档距小于100m时，很少见到振动； 在120m以上时，导线振动就多了一些；在跨越河流，山谷等高杆塔大档距的地方，可以观测到较强烈的振动。
　　综上所述，一般开阔地区易产生平稳、均匀的气流，因而，凡输电线路通过平原、沼地、漫岗、横跨河流和平坦的风道，认为是易振区；且线路走向和全年主导风向 垂直或夹角大于45°时，有较强的振动。
　　(3)应力对振动的影响。由前述已知，导线的应力是影响导线振动烈度的关键因素，且对导线振动的频带宽度有直接影响。
　　导线的自由振动频率与导线的应力成正比，可知静态应力越大，振动的频带宽度越宽，越容易产生振动。另一方面，导线长期受振动的脉动力作用，这相当于一个动态应力叠加在导线的静态应力上，而导线的最大允许应力是一定的。因此可见，静态应力越大，振动越厉害，动态应力越大，对线路的危害越严重。而且，随着静态应力的增大，导线本身对振动的阻尼作用也显著降低。
　　这更加重了振动的烈度，更易使导线材料疲劳，引起断股断线事故。
　　特别是在导线的悬挂点处总是波节点，任何波长下均不变，而且此点导线的静态应力又最大。因此，要求最易使导线振动的可能气象条件下的导线最大允许应力应有所限定。由此可见，为什么前面提到的年平均运行应力也成为了导线的可能控制应力。
　　为此，在线路设计考虑防振问题时，需要选择一个导线长期运行过程中运行时间最多，最有代表性的气象条件，即所谓“年平均气温”气象条件，并规定这个气象条件下导线的实际应力不得超过某一规定值，即“年平均运行应力”。根据运行经验，一般对架空输电线路的导线和避雷的平均运行应力和防振的规定如表2所示：
　　表2　架空输电线路的导线和避雷线的年平均运行应力和防振措施

情况	防振措施	年平均运行应力上限 （瞬时破坏应力，%）
档距不超过500米的开阔地区	不需要	16	12
档距不超过500米的非开阔地区	不需要	18	18
档距不超过102米	不需要	18	18
不论档距大小	护线条	22	——
不论档距大小	防振锤（阻尼线）或 另加护条线	25	25

二 、导线的防振措施 　　1．防振措施
　　根据引起导线振动的原因及其影响和导线振动的破坏机理，考虑防振措施可从以
下两方面着手。
　　（1）设法防止和减弱振动，方法有：
　　　1)设法从根本上消除引起导线振动的的条件，如线路路径避开易振区；年平均运行应力降低到不易发生振动的程度等，但这些措施在实际工程中往往不易实现，甚至不可能。
　　　2)设法利用线路设备本身对导线振动的阻尼作用，以减小导线的振动。如采用柔性横担，偏心导线、防振线夹等。
　　　3)在导线上加装防振装置以吸收或减弱振动能量，消除导线振动对线路的危害。目前我国广泛采用的防振措施是防振锤和阻尼线。
　　（2）提高设备的耐振性能。因为导线振动对线路危害主要是引起线夹出口处导线断股断线，所以提高耐振性能的措施主要有：
　　　1)在线夹处导线加装护线条或打背线，以增加出口附近导线的刚性，减少弯曲应力及挤压应力和磨损，同时也能对导线振动起一定阻尼作用。
　　　2)改善线夹的耐振性能，如要求线夹转动灵活，从而线夹随着导线的上下振动能灵活转动，减小导线在线夹出口处的弯曲应力。
　　　3)在技术、经济条件许可的情况下，尽可能降低导线的静态应力。在实际工程中根据需要可选用一种防振措施或两种以上防振措施配合使用，如对一般输电线路普遍采用防振锤防振；有些线路防振锤同时加装护线条进行防振；对500KV线路的重要跨越档距，有时需专门设计一套综合防振措施。
　　必需指出，从理论上讲，并不是要求导线在任何气象条件下都必需采取防振措施，这取决于导线的实际年平均运行应力大小来决定。如果导线的控制条件为年平均气温，则控制应力为25%σ_cal，从振动角度讲其静态应力为最大，此时必需采取防振措施。但如果导线的控制条件为最大风、覆冰或最低温时，则不一定非要采取防振措施，此时要以控制条件计算出的年平均气温应力大小来决定，只当其值大于22%σ_cal时才必需采取防振措施。具体要求可参见表3-2及有关规程规定。
　　2．防振锤的安装
　　最常用的防振锤形式见书中介绍所示，它是由一段短的钢绞线在其两端各装一个重锤，中间专为装于导线上使用的夹板组成。当导线振动时，夹板随着导线上下移动，由于两端重锤具有较大的惯性而不能和夹板同步移动，致使防振锤的钢绞线不断上下弯曲。重锤的阻尼作用减小了振动的振幅，而钢绞线的变形及股线间的摩擦则消耗了导线振动传给它的能量，从而减小了导线的振动。
　　导线振动的振幅越大，防振锤的钢绞线上下弯曲挠度越大，则消耗的能量越多，振幅减小，防振锤消耗的能量随之下降，最后在能量平衡的条件下导线以很低的振幅振动，这就是防振锤的防振原理，但严格的说防振锤并不是“防振”，而是将振动限制到无危险的范围。
　　从防振锤的防振原理可见，要使防振锤能最大限度的消耗导线振动的能量，就要在防振锤选择和安装时，以防振锤的钢绞线能产生最大挠度为原则。
　　在选择防振锤型号时，首先防振锤的固有频率应与导线可能发生的振动频率范围相适应；其次防振锤的重量要适当，太轻则消振效果差，太重则可能在防振锤安装位置形成新的波节点，另外，还应与导线型号相配合，防振锤的选择见书中所列数据。
　　在确定防振锤安装位置时，其出发点是防振锤在这个位置上应能有效地减弱导线振动。
　　因为导线的振动是沿整档导线呈驻波分布的，导线悬挂点处无论何种频率的振动均为一固定的波节点，因此防振锤应安装在悬点附近，另外，防振锤应安装在波腹点附近，这样防振锤甩动幅度最大，消耗振动能量最多，然而，导线振动的频率和波长并非是惟一的，而是在一定范围内变化，为使防振锤的安装能对各种频率和波长的振动都能发挥一定的防振作用，就应照顾到出现最大及最小波长时，都能起到一定的防振作用，如此自然对中间波长的振动具有更好的防振效果。
　　综上所述，当安装一个防振锤时，其安装位置的确定原则是：在最大波长和最小波长情况下，防振锤的安装位置在线夹出口处第一个半波范围内，并对两种波长的波节点或波腹点具有相同的接近程度，即在这两种情况下，防振锤安装点的“相角”的正弦绝对值相等即|sinθ_m|＝|sinθ_n|，如图所示。
　　　
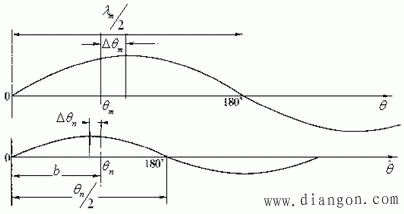
　　　　　　　　　　　　　图防振锤的安装位置
　　导线振动最大半波长产生的条件是：最小振动风速和最大静态应力发生的结果，其关系式表示为
　　　　　　
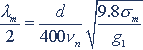
　　　式中　λ_m—振动波的最大波长，m；
　　　　　　v_n —振动的下限风速，m/s；
　　　　　　σ_m—最低气温时导线应力，Mpa。
　　式中σ_m为导线最低气温时的应力，注意到导线在最低温条件时应力不一定是导线最大静态应力，实际也可能是最大风或覆冰条件下使导线受到最大静态应力。
　　但在这两种条件下均不能形成均匀稳定气流，其导线不会振动。因此，能使导线振动且使导线受到最大静态应力气象条件中，则只有最低温条件才成立。
　　同理，导线振动最小半波长产生的条件是：最大振动风速和最小静态应力发生的结果，其关系式表示为
　　　　　　
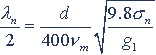
　　　式中　λ_n—振动波的最小波长，m；
　　　　　　v_m —振动的上限风速，m/s；
　　　　　　σ_n—最高气温时导线应力，Mpa。
　　式中σ_n为导线最高气温时的应力，因最高气温条件下能够形成均匀稳定气流可能使导线振动，而此条件下导线的静态应力最小。
　　根据上述原则，当满足|sinθ_m|＝|sinθ_n|时，可以推得防振锤安距离计算式为
　　　　　

　　　式中　b—防振锤的安装距离，m；
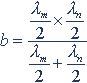
　　防振锤的安装距离b，对悬垂线夹来说，是指自线夹出口至防振锤夹板中心间的距离；对耐张线夹来说，当采用一般轻型螺栓式或压接式耐张线夹时，也指自线夹出口至防振锤夹板中心间的距离。
　　当导线档距较大，悬点高度较高，风的输入能量很大而使导线振动强烈时，安装一个防振锤可能不足以将此能量消耗至足够低的水平，这时就需装多个防振锤。实际工程中，档距两侧各需安装的防振锤个数一般在1－3之间，具体选择见书中介绍。
　　多个防振锤一般均按等距离安装，即按照前述方法计算得第一个防振锤的安装距离b则第二个为2b,第三个为3b。
　　3．阻尼线的安装
　　阻尼线是一种消振性能很好的防振装置，它采用一段挠性较好的钢丝绳或与导线同型号的绞线。平行地敷设在导线下面，并在适当的位置用U形夹子或绑扎方法与导线固定，沿导线在线夹两侧形成递减型垂直花边波浪线。
　　[例3]　某架空输电线路中，有一耐张段各档档距分别为200、360、273m，导线为LGJ－95／20型，导线直径为13.87m,自重比载g₁＝35.187×10^-3N/m·mm²，代表档距l_re＝300m，已知导线最高气温时应力为68.55MPa，最低气温时应力为99.45MPa，试选防振锤型号、安装距离并统计该耐张段所需防振锤个数。
　　解：由书中防振锤型号列表数据，选用FD―2型防振锤。
　　　选振动风速，v_m＝5m/s，v_n＝0.5m/s，则
　　　　
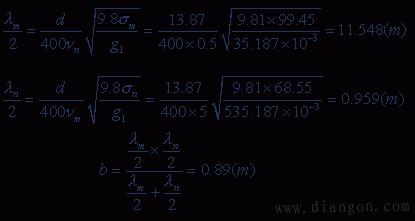
　　　又由书中防振锤安装个数表知，该耐张段所需防振锤个数如下表3所示。
　　　表3防振锤安装表

杆号	1		2		3		4
档距（m）		200		360		273
防振锤个数		3	3	6	6	3	3
安装距离（m）	0.89

　　本文内容主要是涉及架空输电线路设计中有关导线的安装计算问题。通过以上介绍,我们应当了解在架空线路设计中导线安装曲线、导线的初伸长、导线的断线张力以及防振锤的作用等概念，同时能够掌握导线安装曲线计算、 邻档断线交叉跨越距离校验和防振锤安装位置的计算。