若有多位数相加，则可采用并行相加串行进位的方式来完成。例如，有两个4位二进制数A3A2A1A0和B3B2B1B0相加，可以采用两片内含两个全加器或1片内含4个全加器的集成电路组成，其原理图如图1所示。由图可以看出，每1位的进位信号送给下1位作为输入信号，因此，任1位的加法运算必须在低1位的运算完成之后进行，这种进位方式称为串行进位。这种加法器的逻辑电路比较简单，但它的运算速度不高。为克服这一缺点，可以采用超前进位等方式。
 |
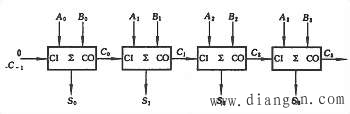| 图1 4位串行进位全加器 |
由于串行进位加法器的速度受到进位信号的限制，人们又设计了一种多位数超前进位加法逻辑电路,使每位的进位只由加数和被加数决定，而与低位的进位无关。现在介绍超前进位的概念。 由表1得Si和Ci的逻辑表达式
 |
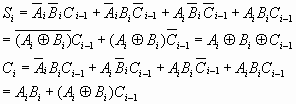| 定义两个中间变量Gi和Pi: | Gi=AiBi |
| Pi=Ai⊕Bi |
 |
 |
 | |
 |
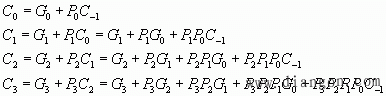同理可推导出S0、S2、S3和CO(C3)的表达式。
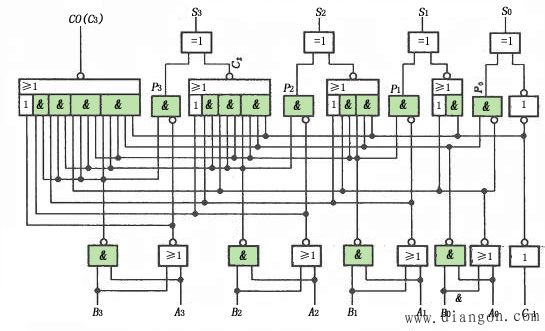
图2 集成4位加法器74LS283
(a)逻辑图
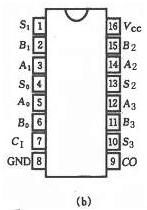（b）引脚图3.超前进位产生器74182
多位数的超前进位加法器的进位是并行产生的，大大提高了运算速度。但是，随着位数的增加，超前进位逻辑电路越来越复杂。为了解决这一矛盾，设计出了专用的超前进位产生器，用多个超前进位产生器连接，既可扩充位数而又不使逻辑电路太复杂。集成超前进位产生器74182的逻辑图和引脚图分别如图3(a)和3(b)所示。
由图3可以对74182的引出端信号说明如下:
74182的输入、输出信号有进位输入端Cn，进位输出端Cn+x、Cn+y、Cn+z，进位产生输出端FG(低电平有效)，进位传输输出端FP(低电平有效)，进位产生输入端G0～G3（低电平有效），进位传输输入端P0～P3（低电平有效）。
74182的逻辑功能如表3(a)～(e)所示
| 表1(a) 74182FG输出功能表 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 表1(b) 74182FP输出功能表 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 表1(c) 74182Cn+x输出功能表 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 表1(d) 74182Cn+y输出功能表 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 表1(e) 74182Cn+z输出功能表 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
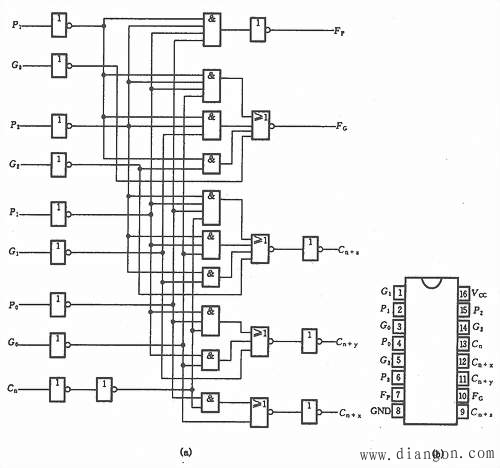图3 集成超前进位产生器74182(a)逻辑图（b）引脚图由图3(a)可得
 |
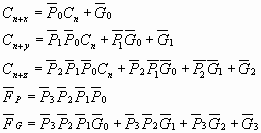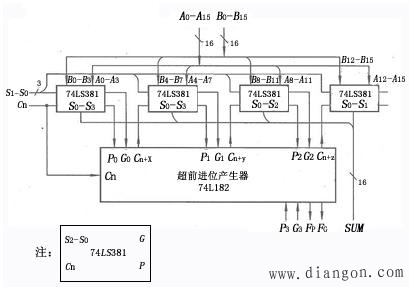图4 16位全超前进位算术/逻辑运算电路