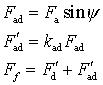1.由零功率因数和空载特性确定定子漏抗和电枢反应磁动势
由于在空载特性曲线与零功率因数特性曲线之间存在着一个不变的特性三角形,因此,前面已介绍过由已知特性三角形和一条特性曲线(设为空载特性)求另一条特性曲线(设为零功率因数特性)的方法。现在,如果已知条件为两条特性曲线,那么,可不可以由此求出它们之间的特性三角形呢?答案是肯定的,具体作法如下。
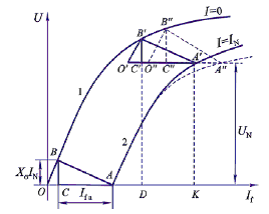
图1 零功率因数和空载特性确定定子漏抗和电枢反应磁动势
设图1 中的曲线1和2分别为已知空载特性曲线(I=0)和理想的零功率因数特性曲线(I=IN)。这里的所谓“理想”,指的是零功率因数特性与空载特性之间严格存在一个大小恒定的特性三角形。现在曲线 2 上取额定电压点 A′(也可任选),过 A′作 AO 的平行线 A′O′,且使 A′O′= AO ,再过 O′作平行于空载特性起始段的直线O′B′交曲线 1 于 B′,连 B′A′ 并作B′C′垂直于 A′O′并交 A′O′于 C′,则三角形 A′B′C′即为所求。平移至短路点即为三角形ABC,于是有 AC =Ifa, BC = INXσ 或 Xσ= BC / IN 。
2.保梯电抗Xp(PotierReacfance)
首先考虑空载且 If=OD的情况。此时励磁电流除产生气隙磁通并在定子绕组感应出空载气隙电动势 Eδ=E0= DB′外,还产生少量的主极漏磁通。
当电机在纯电感负载下运行且 If=OK、Ifa=kadFa/Nf= DK时,虽然产生气隙合成磁通所对应的等效励磁电流 If 依然是OD,与空载时相同,但主极漏磁情况却发生了变化。空载时主极漏磁对应于OD,纯感性负载时对应于OK,而OK>OD,说明主极漏磁增多,转子磁极和磁轭两段磁路的实际饱和程度增高,整个主磁路上的磁阻也就变大,尽管气隙合成磁动势相同,但气隙合成磁通会略有减少,致使实际的 Eδ< DB′,在扣除漏抗压降 B′C′之
后使端电压小于 DC′ 。这说明同样励磁电流下实际零功率因数特性曲线会低于理想化曲线,并随主磁路饱和程度加深而更趋明显。
由此可见,当用实测零功率因数特性作图求得特性三角形 A″B″C″时,结果会是A″C″ < A′C′ ,即所得电枢反应等效励磁电流 Ifa′<Ifa,但 B″C″>
综上,考虑主磁路饱和对转子漏磁的影响,特性三角形不是恒定不变的。对应于短路点,称之为短路三角形(即图中的三角形 ABC),而对应于额定点处称之为保梯三角形。保梯电抗大于漏电抗。对隐极机,Xp=(1.05~1.10)Xσ;对凸极机,有 Xp=(1.1~1.3)Xσ。
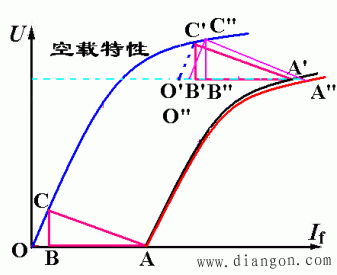
图2 零功率因数和空载特性确定保梯电抗
3.短路比的概念
当发电机空载运行时,空载电动势等于额定电压UN时,所加的励磁电流 if0,保持此励磁电流不变,在稳态短路时所对应电流为IK,IK与发电机额定电流IN之比,称为短路比Kc 。
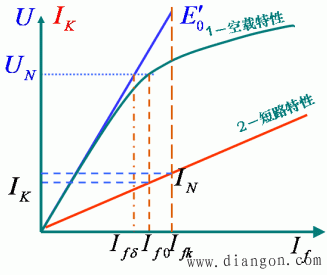
图3 空载特性和短路特性确定短路比
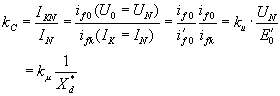
短路比和发电机的性能
分析:短路比略大于不饱和同步电抗的倒数
短路比大,则同步电抗小,负载变化时发电机的电压变化就小,并联运行时发电机的稳定度较高;设计上,电机气隙较大,转子的额定激磁磁势和用铜量增大,成本增加。
短路比小,同步电抗大,负载变化时发电机的电压变化就大——电压调整率大,发电机的稳定度较差。
工程上:
随着单机容量的增大,为了提高材料利用率,随机组容量增大短路比降低。
由于采用自动励磁调节装置,大大提高了运行稳定性,降低短路比可以提高电机经济指标。
4.Xd的不饱和值
由空载及短路特性求取同步电抗
从特性曲线图上我们可以看出:在不饱和区间,即当if=if1很小时,运行于空载特性不饱和部分(直线部分),那么E01与Ik1之比求得的是同步电抗的不饱和值。
短路时不计饱和
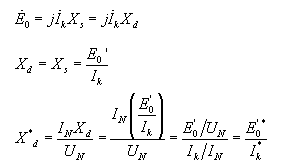
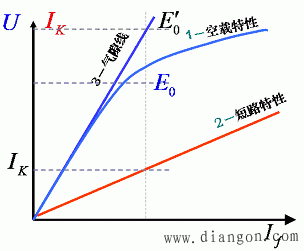
图4 空载特性和短路特性确定Xd的不饱和值
在凸极电机中,通过开路试验及短路试验只能求出直轴同步电抗。根据经验公式,可以得到交轴同步电抗为:
![]()
5.Xd的饱和值由空载特性和零功率因数特性确定
饱和同步电抗
磁路饱和决定于空气隙中的合成磁场,
![]()
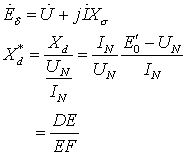
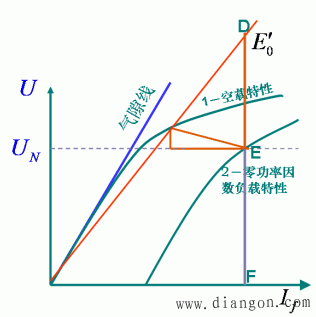
图5 由空载特性和零功率因数特性确定Xd的饱和值
6.电压调整率和额定励磁磁动势的求法
(1)由矢量图求取凸极同步电机的电压调整率和额定励磁磁动势。

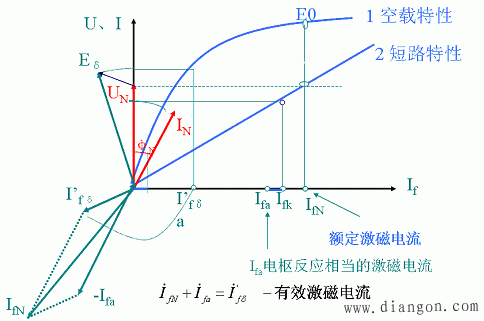
图6 由矢量图求取凸极同步电机的电压调整率和额定励磁磁动势
(2)由矢量图求取隐极同步电机的电压调整率和额定励磁电流

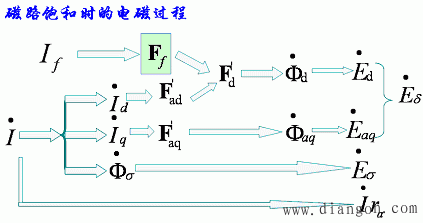
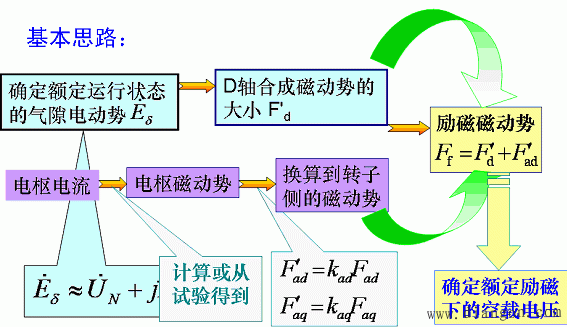
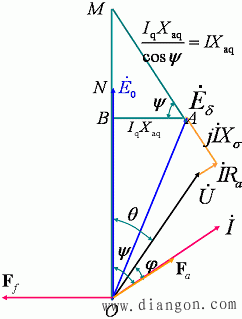
图7 由矢量图求取隐极同步电机的电压调整率和额定励磁电流
已知额定负载时U=UN,I=IN,con![]() N, Ra, Xp, Kad, Kaq
N, Ra, Xp, Kad, Kaq
(1)求气隙电动势
![]()
(2)确定AM的长度,即确定q轴的位置。(q轴不饱和,利用空载特性的气隙线)

(3)d轴合成电动势Ed:连接OM,过A作OM的垂直线AB,OB即为Ed
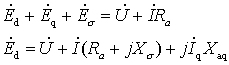
(4)由合成电动势Ed确定d轴的合成磁动势Fd′(利用空载特性)
(5)确定额定励磁磁动势Ff, E0