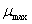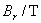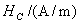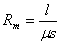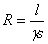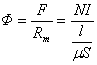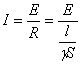磁路及其分析方法

1、磁场的基本物理量

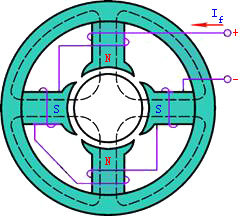
在变压器、电机、电磁铁等电工设备中常用磁性材料做成一定形状的铁心。铁心的磁导率比周围空气或其他物质的磁导率高得多，因此铁心线圈中电流产生的磁通绝大部分经过铁心而闭合。这种磁通的闭合路径，称为磁路。图1和图2分别表示四极直流电机和交流接触器的磁路。磁通经过铁心(磁路的主要部分)和空气隙(有的磁路中没有空气隙)而闭合。

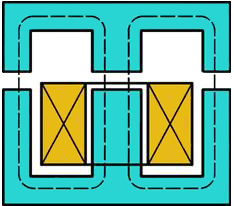图1直流电机的磁路	图2交流接触器的磁路

磁路问题也是局限于一定路径内的磁场问题。磁场的特性可用下列几个基本物理量来表示。

(1) 磁感应强度

磁感应强度B是表示磁场内某点的磁场强弱和方向的物理量。它是一个矢量。它与电流(电流产生磁场)之间的方向关系可用右手螺旋定则来确定。

如果磁场内各点的磁感应强度的大小相等，方向相同，这样的磁场则称为均匀磁场。

(2) 磁通

磁感应强度B(如果不是均匀磁场，则取B的平均值)与垂直于磁场方向的面积S的乘积，称为该面积的磁通Φ，即

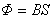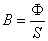或　　　(1)

由上式可见，磁感应强度在数值上可以看成为与磁场方向垂直的单位面积所通过的磁通，故称为磁通密度。

根据电磁感应定律的公式

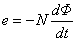
可知，磁通的单位是伏秒(V·s)，通常称为韦[伯](Wb)。

磁感应强度的单位是特[斯拉](T)，特[斯拉]也就是韦[伯]每平方米(Wb/)。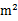

(3) 磁场强度

磁场强度H是计算磁场时所引用的一个物理量，也是矢量，通过它来确定磁场与电流之间的关系。

磁场强度的单位是安[培]每米(A/m)。

(4) 磁导率

磁导率μ是一个用来表示磁场媒质磁性的物理量，也就是用来衡量物质导磁能力的物理量。它与磁场强度的乘积就等于磁感应强度，即

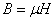　　　(2)

磁导率μ的单位是亨[利]每米(H/m)。即

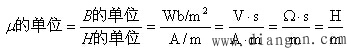
式中的欧秒(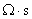)又称亨[利](H)，是电感的单位。

由实验测出，真空的磁导率

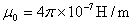
因为这是一个常数，所以将其他物质的磁导率和它去比较是很方便的。

任意一种物质的磁导率μ和真空的磁导率μ0的比值，称为该物质的相对磁导率μr，即

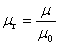　　　(3)

1.2 磁性材料的磁性能

分析磁路首先要了解磁性材料的磁性能。磁性材料主要是指铁、钴、镍及其合金，常用的几种列在表1中。它们具有下列磁性能。

(1) 高导磁性

磁性材料的磁导率很高，μr>>1，可达数百、数千、乃至数万之值。这就使它们具有被强烈磁化(呈现磁性)的特性。

由于高导磁性，在具有铁心的线圈中通入不大的激励电流，便可产生足够大的磁通和磁感应强度。这就解决了既要磁通大，又要激励电流小的矛盾。利用优质的磁性材料可使同一种容量的电机的重量和体积大大减轻和减小。

表1常用磁性材料的最大相对磁导率、剩磁及矫顽磁力

(2) 磁饱和性

将磁性材料放入磁场强度为H的磁场(常为线圈的励磁电流产生)内，会受到强烈的磁化，其磁化曲线(B-H曲线)如图3.3所示。开始时，B与H近于成正比地增加。而后，随着H的增加，B的增加缓慢下来，最后趋于磁饱和。

磁性物质的磁导率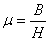，由于B与H不成正比，所以μ不是常数，随H而变(图3)。

由于磁通Φ与B成正比，产生磁通的励磁电流I与H 成正比，因此存在磁性物质的情况下，Φ与I也不成正比。

(3) 磁滞性

当铁心线圈中通有交流电时，铁心就会受到交变磁化。在电流变化时，磁感应强度B随磁场强度H而变化的关系如图4所示。有图可见，当H已减到零时，B并未回到零值。这种磁感应强度滞后于磁场强度变化的性质称为磁性物质的磁滞性。图4所示的曲线也就是磁滞回线。

当线圈中电流减到零值(即H=0)时，铁心在磁化时所获得的磁性还未完全消失。这时铁心中所保留的磁感应强度称为剩磁感应强度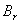(剩磁)，在图4中即为纵坐标O-2和O-5，永久磁铁的磁性就是由剩磁产生的。但对剩磁也要一分为二，有时它是有害的。例如，当工件在平面磨床上加工完毕后，由于电磁吸盘有剩磁还将工件吸住。为此，要通入反向去磁电流，去掉剩磁，才能将工件取下。再如有些工件(如轴承)在平面磨床上加工后得到的剩磁也必须去掉。

如果要使铁心的剩磁消失，通常改变线圈中的励磁电流的方向，也就是改变磁场强度H的方向来进行反向磁化。使B=0的H值，在图4中用O-3和O-6代表，称为矫顽磁力。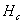

图4 磁滞回线	图4B 和μ与H的关系

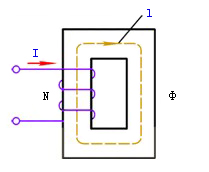
3、磁路的分析方法

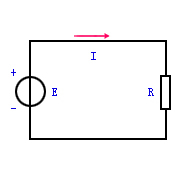
以图5所示的磁路为例，根据安培环路定律

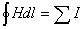
可得出

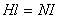　　　(4)

式中，N是线圈的匝数，l是磁路(闭合回线)的平均长度，H是磁路铁心的磁场强度。

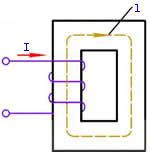图5 磁路

上式中线圈匝数与电流的乘积NI称为磁通势，用字母F代表，即

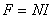　　　(5)

磁通就是由它产生的。它的单位是安[培](A)。

将H=B/μ和B=Φ/S代入式4)，得

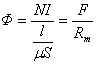　　　(6)

式中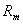，称为磁路的磁阻，S为磁路的截面积。

式(6)与电路的欧姆定律在形式上相似，所以称为磁路的欧姆定律。两者对照，见表2。

表2 磁路与电路对照

磁路	电路
磁通势F	电动势E
磁通Φ	电流I
磁感应强度B	电流密度J
磁阻	电阻

由于式(6)中的μ不是常数，所以该式只能用于定性分析，不能用于定量计算。计算均匀磁路可用式(4)。如果磁路是由不同的材料或不同长度和截面积的几段组成的，利用下式计算

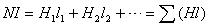　　　(7)