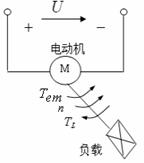
图1单轴电力拖动系统
旋转运动的方程式为
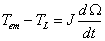 (1)
(1)
式中,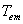 为电动机产生的拖动转矩(
为电动机产生的拖动转矩(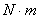 );
);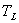 为负载转矩(
为负载转矩(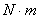 );
);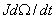 为惯性转矩(或称动转矩),
为惯性转矩(或称动转矩),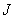 为转动惯量可用下式表示
为转动惯量可用下式表示
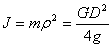 (2)
(2)
式中,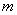 .
.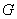 分别为旋转部分的质量(
分别为旋转部分的质量(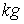 )与重量(
)与重量(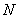 );
);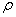 .
.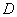 分别为转动惯性半径与直径(
分别为转动惯性半径与直径(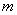 );
);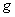 为重力加速度,
为重力加速度,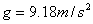 ;
;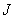 的单位为
的单位为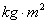 。
。
需要说明的是,式(1)中忽略了电动机本身的损耗转矩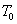 ,认为电动机产生的电磁转矩全部用来拖动负载。这一点将在以后的内容详细介绍。
,认为电动机产生的电磁转矩全部用来拖动负载。这一点将在以后的内容详细介绍。
在实际计算中常用式(1)的另一种形式。即将角速度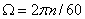 (
(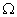 的单位为
的单位为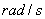 ,
,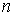 的单位为
的单位为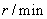 )代入式(1)得运动方程式实用形式:
)代入式(1)得运动方程式实用形式:
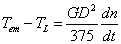 (3)
(3)
式中,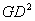 为飞轮矩(
为飞轮矩(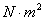 ),
),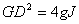 ;系数
;系数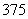 是具有加速度量纲的系数。
是具有加速度量纲的系数。
电动机的转子及其他转动部件的飞轮矩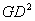 的数值可由相应的产品目录中查到,但是应注意将单位
的数值可由相应的产品目录中查到,但是应注意将单位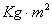 化成国际单位制
化成国际单位制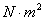 (乘以
(乘以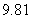 )。
)。
电动机的工作状态可由运动方程式表示出来。分析式(3)可见
(1)当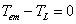 ,
,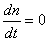 ,则
,则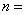 常值,电力拖动系统处于稳定运转状态;
常值,电力拖动系统处于稳定运转状态;
(2)当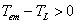 ,
,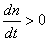 ,电力拖动系统处于加速过渡过程状态中;
,电力拖动系统处于加速过渡过程状态中;
(3) 当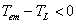 ,
,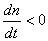 ,电力拖动系统处于减速过渡过程状态中。
,电力拖动系统处于减速过渡过程状态中。
运动方程式中转矩的符号分析
应用运动方程式,通常以电动机轴为研究对象。由于电动机运转状态的不同以及生产机械负载类型的不同,电动机轴上的拖动转矩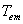 及负载转矩
及负载转矩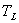 不仅大小不同,方向也是变化的。运动方程式可写成下列一般形式:
不仅大小不同,方向也是变化的。运动方程式可写成下列一般形式:
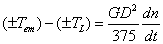 (4)
(4)
式(4)中拖动转矩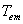 及负载转矩
及负载转矩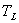 前均带有正负符号,并作如下规定:
前均带有正负符号,并作如下规定:
如设定电力拖动系统的正方向,则拖动转矩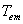 的方向如果与所设定的正方向相同,
的方向如果与所设定的正方向相同,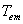 前带正号,相反时带负号。在式(4)中,由于负载转矩
前带正号,相反时带负号。在式(4)中,由于负载转矩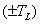 前已带有负号,因此其正负号的规定恰与拖动转矩
前已带有负号,因此其正负号的规定恰与拖动转矩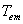 的规定相反。即当负载转矩
的规定相反。即当负载转矩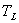 的方向与设定的旋转正方向相同时,负载转矩
的方向与设定的旋转正方向相同时,负载转矩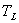 前取负号,相反时则取正号。本书的计算中,均规定电力拖动系统的正向电动机转向为系统的正方向。
前取负号,相反时则取正号。本书的计算中,均规定电力拖动系统的正向电动机转向为系统的正方向。
上面的规定也可归纳为:拖动转矩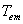 与规定正向相同取正,相反取负;负载转矩
与规定正向相同取正,相反取负;负载转矩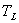 与规定正向相同取负,相反取正。
与规定正向相同取负,相反取正。
惯性转矩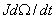 的大小及正负符号由拖动转矩
的大小及正负符号由拖动转矩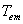 及负载转矩
及负载转矩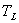 的代数和来决定。
的代数和来决定。
