电阻电路与正弦稳态电路相量法分析比较:


可见在用相量法分析计算时,引入正弦量的相量、阻抗、导纳的概念,其元件的VCR方程和KCL、KVL的相量形式在形式上与线性电阻电路相似。
因此,用相量法分析时,线性电阻电路的各种分析方法和电路定理可推广用于线性电路的正弦稳态分析,差别仅在于所得电路方程为以相量形式表示的代数方程以及用相量形式描述的电路定理,而计算则为相量(复数)运算。显然两者描述的物理过程之间有很大差别。
一般正弦交流电路的解题步骤:
1.据原电路图画出相量模型图(电路结构不变);
![]()
2.根据电路的相量模型列出相量方程式或画相量图;
3.用相量法或相量图法求解;
4.将结果变换成要求的形式。
例1. 列写电路的回路电流方程。
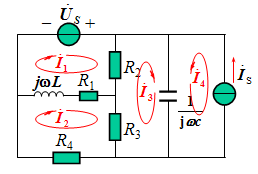
解:
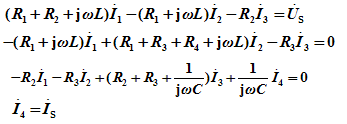
例2. 列写电路的节点电压方程。
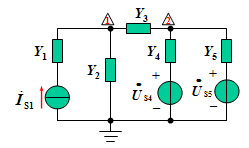
解:
节点1:
![]()
节点2:
![]()
例3.列出右图电路的结点电压方程和回路电流方程。
解:结点顺序号如图所示,以结点d为参考结点。
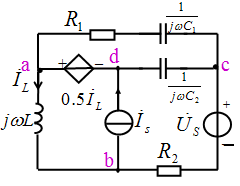
(1)列结点电压方程。
结点a:![]()
附加方程:![]()
结点b:![]()
结点c: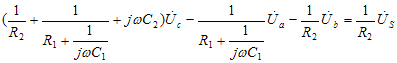
(2)列回路电流方程。独立回路顺序号及绕向如图所示:
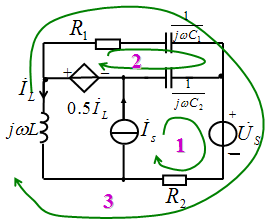
回路1:![]()
附加方程:![]()
回路2:![]()
回路3:![]()
例4.
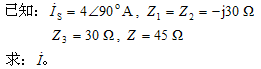
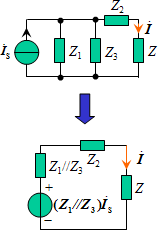
解:方法1:电源变换。
![]()
![]()
![]()
![]()
![]()
方法2:戴维宁等效变换。
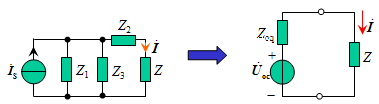
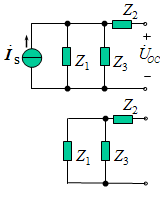
(1)求开路电压。
![]()
(2)求等效电阻。
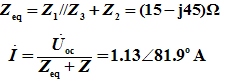
例5. 用叠加定理计算电流![]() 。
。
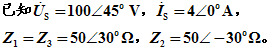
解:

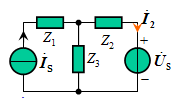
例6.已知平衡电桥Z1=R1 , Z2=R2 , Z3=R3+jωL3 。 求:Zx=Rx+jωLx。
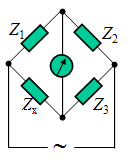
解:由电桥平衡条件:Z1Z3= Z2Zx,得:
R1(R3+jωL3)=R2(Rx+jωLx)
∴ Rx=R1R3 /R2 Lx=L3 R1/R2
正弦稳态电路电桥平衡条件:
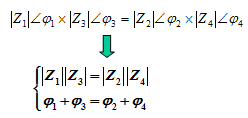
例7.已知:Z=10+j50Ω, Z1=400+j1000Ω 。
![]()
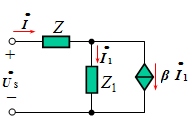
![]()
![]()
解:

