1、结点分析方程
【结点电位】在有n个结点的电路中，任选一个结点为参考结点，其余各结点至参考结点的电压称为该结点的结点电位。
【结点分析法】以结点电位为待求变量，将各支路电流用结点电位表示，列写除了参考结点以外其他所有结点的KCL方程，求得结点电位后再确定其他变量的电路分析方法，称为结点分析法，简称结点分析法。
【结点分析方程的列写步骤】
（1）选取参考结点，假定其余n-1个独立结点的结点电位。
（2）列写n-1个独立结点的KCL方程，方程中的各支路电流用结点电位表示。
（3）求解方程，得到结点电位。
（4）通过结点电位确定其他变量。
【例3-1-1】对图3-1-1所示电路列写结点方程。
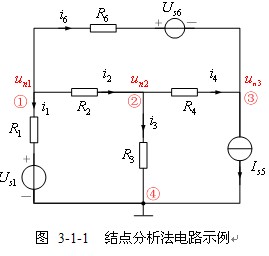
解：设结点④为参考结点，并令独立结点①、②、③电压分别设为
、
、
。分别列写结点①、②、③的KCL方程如下。
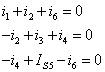
为得到以结点电位为未知变量的电路方程，用结点电位表示各支路电流，即有
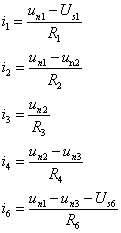
将上述各式代入KCL方程，得到结点方程
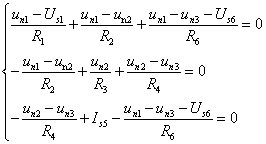
整理得
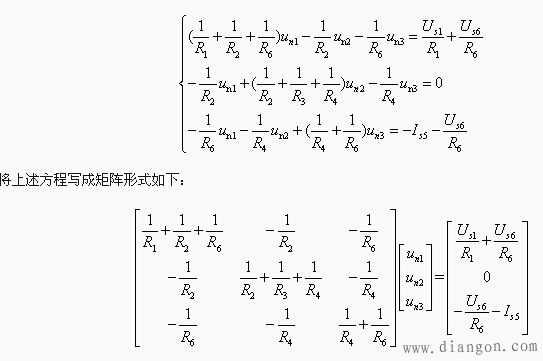
【结点自电导】矩阵中对角线元素 
是与结点①所有相联支路电导之和，对角线元素
，
分别是结点②、③的所有相联支路电导之和。对角线元素称为结点自电导。
【结点互电导】非对角线元素，如第一行、第二列元素，是结点①、②之间公共支路电导之和的负值，其余非对角线元素也满足相似的规律，称为结点互电导。
【结点等效电流源】等式右边是流入各结点的电流源，包括电压源通过戴维宁支路变换为诺顿支路所得的等效电流源，之电流的代数和，流入结点取正值，反之取负值。
2、结点方程的视察列写
【结点方程的一般形式】对具有n个结点的电路，其结点方程可写为如下矩阵形式：
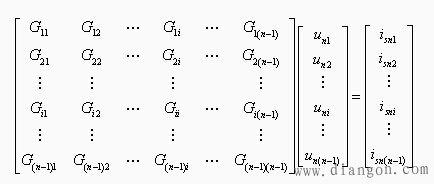
或写成矩阵形式 
其中：
结点自电导
＝与结点i相联的所有支路电导之和，恒是为正值。
结点互电导
＝结点k、j之间公共支路的电导之和的负值，对于不含受控电源的电路，结点互电导恒是为负值或为零。
结点等效电流源
＝结点i相联的电流源、包括由电压源等效转换而来的电流源之电流的代数和，流入结点取正值，反之取负值。
【结点电导矩阵】
为结点导纳矩阵。对于不含受控电源的电路，为对称矩阵。
【结点方程的视察列写法】根据上述结点自电导、互电导、等效电流源的含义和确定方法，可以直接从电路写出结点方程的最终形式，而不需要通过“列写n-1个独立结点的KCL方程，方程中的各支路电流用结点电位表示”的过程得到结点方程。根据自电导、互电导、等效电流源的含义直接得到结点方程的最终形式的方法称为视察列写法。
3、含受控源电路的结点方程
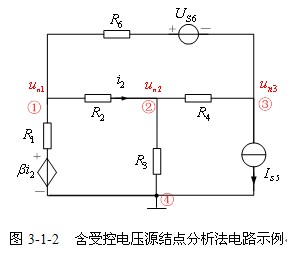
【含受控源电路的结点分析方程】在列写结点方程时，受控电源可以和独立电源一样处理，差别在于最后要把受控电源的控制量用结点电位表示。将图3-1-1中独立电压源
用一受控电压源
代替，如图3-1-2所示。此时，例3-1-1的结点方程中, 用代替，即
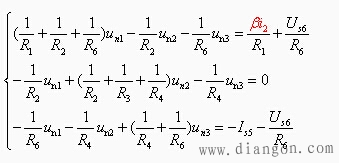
该结点方程中出现了控制变量
，可以用结点电位表示
代入上式并整理将结点电位归并到方程左边
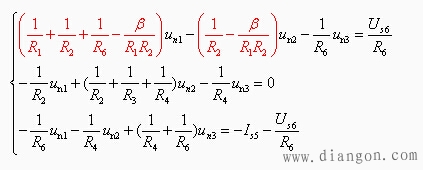
4、含无伴电压源支路的电路的结点方程
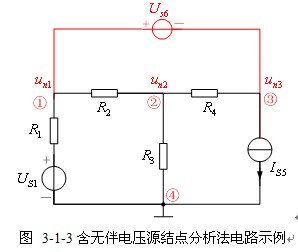
将图3-1-1中独立电压源
与电阻
串联支路变为无伴电压源支路，如图3-1-3所示，该支路的电阻为零，电导无穷大，支路电流不能用结点电位表示。下面介绍两种处理方法。
【解法一】选择与无伴电压源支路相连的一个结点作为参考结点。如图3-1-4所示。则无伴电压源支路的另一结点电位由无伴电压源决定，该结点方程（KCL方程）可不列写。在本例中选择结点③为参考结点，则有
只需列写结点②、④的方程
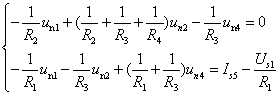
【解法二】做包围无伴电压源的两个结点的封闭面S（即广义结点，实为割集）。如图3-1-5所示。对该封闭面列写KCL方程，得到广义结点方程
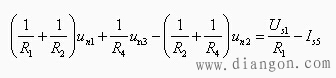
再加上结点②的结点方程和附加方程
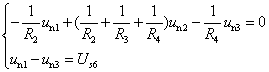
由这三个方程可以求解结点电位、、。
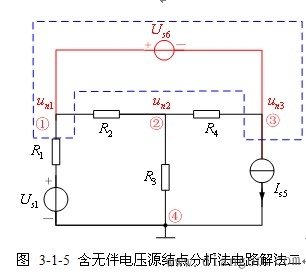
【结点分析法的实质】结点分析法的实质是以结点电位为待求变量，列写n-1个独立的KCL方程，对结点数少的电路尤为适用。一旦选定了参考结点，则其余结点相对于参考结点的电压即为结点电位，未知量非常容易确认，因此在电路计算机辅助分析中多采用结点分析法。