1、网孔分析方程
【网孔电流】根据电流的连续性，可以假定一个电流在指定的网孔中流动，这种电流称为网孔电流，对于电路中每一个结点，网孔电流流入一次又流出一次，所以当以网孔电流作为电路待求变量时，电路的KCL方程自动满足，只需列写b-n+1个网孔的KVL 方程。
【网孔分析法】以网孔电流为待求变量，按KVL建立方程求解电路的方法称为网孔分析法。其网孔电流方程也称为网孔方程。
【例3-2-1】图3-2-1所示电路列写网孔方程。
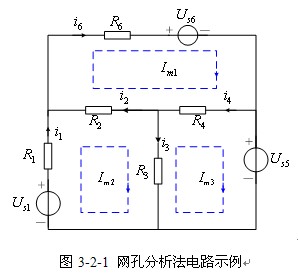
解：假定网孔电流
分别在网孔1、2、3中流动，网孔电流的参考方向如图3-2-1所示。
以支路电流为变量，列写各网孔的KVL方程为
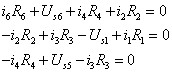
为得到以网孔电流为未知变量的电路方程，用网孔电流表示各支路电流，即有
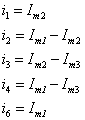
将上述各式代入KVL方程，可得网孔电流方程
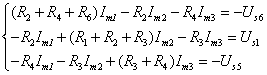
即为该电路的网孔方程，显然，由此三个方程，可求解网孔电流。
2、网孔方程的视察列写
【网孔方程的一般形式】将例3-2-1的网孔方程推广到有m个网孔的电路，其网孔方程可写成矩阵形式
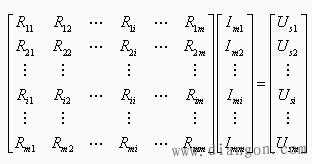
式中：
为网孔i的自电阻，等于组成网孔的各支路电阻之和。
为网孔j，k的互电阻，等于网孔j，k公共支路上电阻之和的负值，在此假定所有网孔的绕向相同，因此相邻网孔的网孔电流以相反的参考方向流过公共支路。否则上述规律不成立。
为网孔i的网孔电流。
为网孔i的等效电压源，等于网孔i中所包含的电压源，包括电流源通过诺顿支路变换为戴维宁支路所得的等效电压源，之电压的代数和，与网孔电流方向非关联者取正值，反之取负值。
【网孔方程的视察列写法】根据网孔自电阻、互电阻、等效电压源的含义和计算方法，可以直接列写网孔分析方程的最终形式，称为视察法。不必通过上述“按KVL建立网孔方程、并将电压用网孔电流表示”的过程得到网孔分析方程。
【含受控源电路的网孔方程】对含受控电压源的电路，先将受控源视为独立电源，依照视察法的规律列写网孔方程，然后将受控源的控制量用网孔电流表示出来。
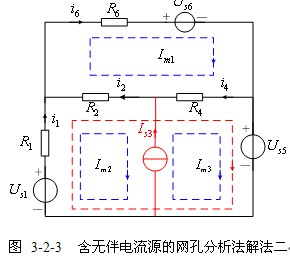
3、含无伴电流源支路的电路的网孔方程
如图3-2-2所示，将图3-2-1中电阻
支路变为无伴电流源支路，该电流源支路的电压无法用网孔电流表示，下面介绍处理方法。
【解法一】设无伴电流源端电压
为待求变量。在列写方程时，无伴电流源支路相当于电压为的“电压源”。3个网孔电流方程为
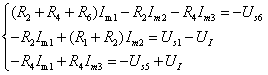
方程有4个未知量，只有3个方程。需增补一个无伴电流源对相邻两网孔的约束方程，即
由这四个方程可以求解出网孔电流。
【解法二】列写由两个包含无伴电流源网孔组合而得的回路的KVL方程，用它取代两个包含无伴电流源网孔的KVL方程，从而避开无伴电流源支路。如图3-2-3所示红色回路即是由两个包含无伴电流源的网孔
，
组合而得的回路，该回路的KVL方程为
再结合网孔的方程
以及无伴电流源对相邻两网孔的约束方程
由以上3个方程求解网孔电流。
