1．戴维南和诺顿电路
图1(a)、(b)表示两种典型的含独立源一端口电路，其中电压源
和电阻
串联的电路称为戴维南 电路；电流源
和电导
并联的电路称为诺顿电路。在端口电压、电流取非关联参考方向的条件下，它们的电压、电流关系分别为
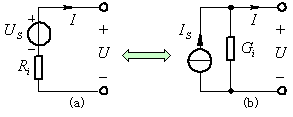
图1 戴维南电路与诺顿电路的等效变换
戴维南电路的端口特性方程：
，
诺顿电路的端口特性方程：
，
对诺顿电路方程进行变形为：
所以等效条件为：
注：电压源内阻Ri=0，而电流源内导Gi=0时，即内阻等于无穷大，它们也称为理想电源。零不能取倒数，故电压源和电流源不能相互等效 。
2．其它含源支路的等效
（1）电压源并联电阻（解释清楚端口上的电压、电流变换前后的关系，“等效”只是对外部电路(不包含被变换部分)而言）
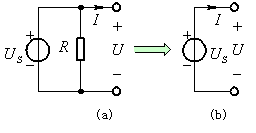
图2 电压源与电阻并联
（2）电流源串联电阻
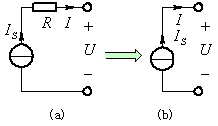
图3 电流源与电阻串联
（3）含受控源支路的等效
图4 含受控源电路的等效变换
注：受控源支路变换方法与含独立源的情况相似。但在使用这种变换时注意不要使控制量消失。
例题1：用等效变换求图示电路中电流I。
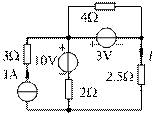
图2.10 例题2.2
解：1、将电流源与电阻串联电路等效成电流源，将电压源与电阻并联电路等效成电压源，将电压源与电阻串联支路等效成电流源与电阻并联支路
2、将两个并联电流源等效为一个电流源，其源电流等于两个并联电流源源电流的代数和
3、将电流源与电阻并联电路等效成电压源与电阻串联支路，并将两个串联电压源等效成一个电压源。
4、由等效电路计算电流I
例题2：利用等效变换求图示电路的电流
。
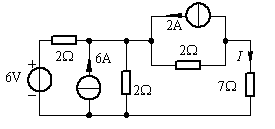
图 题2.11例题2
解： (1)将电压源串电阻等效为电流源并电阻，如图(a-1)；
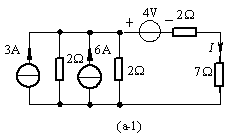
(2)将两并联电流源电流相加，两
电阻并联等效为
电阻，
电流源与
电阻并联等效为
电压源与
电阻串联，如图(a-2)；
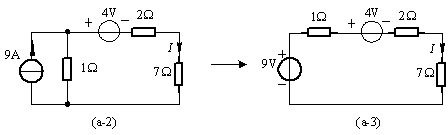
(3)再等效成图(a-3)，由(a-3)求得
注释：从远离待求电流I的地方向电流I处等效。