集成运放在信号运算电路中的应用

如前所述，当运算放大器工作在线性区时，输出电压和输入电压满足式的线性关系。由于运算放大器的开环电压放大倍数A_uo 非常高，即使输入毫伏级以下的信号，也足以使输出电压达到饱和。另外，由于干扰使工作难于稳定，所以要使运算放大器工作在线性区，通常要引入深度电压负反馈。
运算放大器能对输入信号进行比例、加、减、积分和微分、对数与反对数以及乘除等运算。下面介绍几种简单的运算电路。
1．比例运算电路
比例运算电路，根据输入方式的不同，分为反相比例运算电路和同相比例运算电路。
（1）反相比例运算电路
图所示是反相比例运算电路。输入信号u_i 经电阻R₁ 加到反相输入端，同相输入端经R₂ 接地， R_f为反馈电阻。
下面分析该电路的运算关系。根据虚断， R₂上无信号压降，u₊ =0；又根据虚短，则 u_-=u₊=0，因此反相端的电位等于地电位，可把它看成与地相接，但又不是真的接地，故称为虚地。

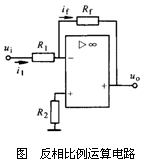
由于反相端虚地，则

又因为虚断，则i_i=i_f ，故有

此式表明，当反相输入的运放A_uo 足够大时，整个电路的闭环电压放大倍数A_uo 仅由外接电阻之比R_f /R_l 来决定，而与运放本身的A_uo 无关，只要阻值R_fR_l 足够精确与稳定，输出电压与输入电压的比例关系也就足够精确与稳定。式中的负号表示u_o 与u_i 反相。当 R_l=R_f 时，u_o =－u_i ，该电路就构成了反相器或称反号器。
上图中的R₂ 为平衡电阻。在运放的实际应用中，为了保证其输入级差放的两个输入端的外接电路结构对称，同相端并不直接接地，而是通过平衡电阻接地。图中的R₂ = R_l∥R_f 。
（2）同相比例运算电路
下图所示是同相比例运算电路。信号u_i 由同相端输入，反相输入端通过电阻R_l 接地， R_f是反馈电阻。
根据虚断有

根据虚短，u₊ =u_- 所以


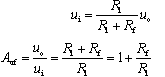
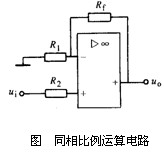
这说明输出电压与输入电压成比例且相位相同，电压放大倍数≥1 ，这是与反相比例运算电路所不同的。
同前所述，为使之平衡，应使电阻 R₂ = R_l∥R_f 。
上式中，当R_l=∞ （开路）或R_f =0（短路）时， ，则有


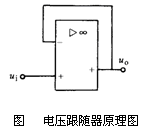
显然，输出电压跟随着输入电压作相同变化，故称其为电压跟随器，或称同号器，如上图所示。电压跟随器的电压放大倍数接近于1，这与射极跟随器相似，它的输入电阻非常高，输出电阻又非常低，这是普通射极跟随器所难以达到的，其性能更接近于理想的电压跟随器，在电路中常用作隔离电路使用。
2．加法运算电路
下图所示是反相输入方式的加法运算电路。信号电压均通过电阻接在电路的反相输入端。
由于反相端虚地，可得

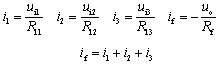
故有

图中的平衡电阻 ，当 时，上式为

若在后面再接一级反相器，就可消去负号，实现几个信号的代数相加。

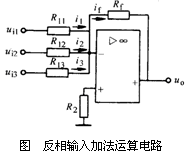
3．减法运算电路（差动运算电路）
前述的运算电路，信号电压都是从运放的单端输入的。如果两个输入端都有信号，则为差动输入。差动输入电路如图所示。
差动输入运算电路可以看作是反相输入与同相输入比例运算电路的组合。在线性工作条件下，可以用叠加原理来分析该电路的运算关系。

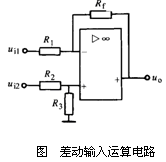
当 单独作用（=0 ）时，为反相输入电路，其输出

当u_i2 单独作用（u_i1 =0）时，为同相输入电路，其输出

然后叠加，，故得

当 时，上式为

即输出电压与两输入电压的差值成正比。当 时，得if

即成为减法器。被减数 u_i2接在同相端，而减数u_i1 接在反相端。
4．积分运算电路
图所示是积分运算电路。根据虚断和虚短， ，这个电流对电容C进行充电


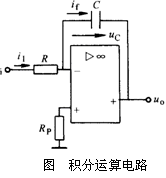
输出电压为

即输出电压和输入电压之间有积分关系。式中，t=RC ，为积分时间常数。
当信号电压 u_i为阶跃电压U_i 时，输出电压u_O 与时间t成线性关系，即

由于积分电路的最大输出电压为±U_Om ，故其有效积分时间t_m 为


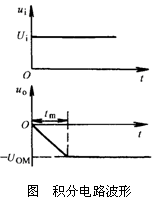
超过t_m 时间后，积分不能继续进行，u_o 将达到输出饱和电压（设±U_O=±U_Om ），如右图所示。如果要使有效积分时间增加，可用改变时间常数的方法来实现。
5．微分运算电路
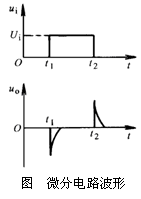
微分是积分的逆运算，将积分运算电路的电容与电阻互换位置，便可构成微分运算电路，如图

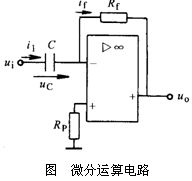
所示，由图可以看出

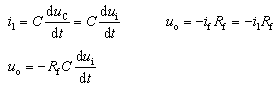
即输出电压与输入电压对时间的一次微分成正比。
当输入电压为一矩形波时，仅在u_i 发生跃变时运放才有尖峰电压输出，而当输入电压不变时，运放将无输出。输出尖峰电压幅度不仅与R_fC 的大小有关，而且还取决于u_i 的变化率。因为运放的输出为有限值，故尖峰电压的幅度不可能为无穷大，其波形如下图所示。