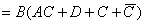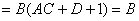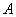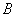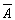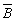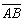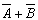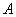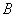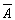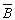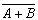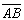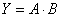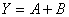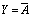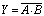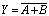逻辑代数或称布尔代数,它是分析与设计逻辑电路的数字工具。它虽然和普通代数一样也用字母(A,B,C,…)表示变量,但变量的取值只有1和0两种,所谓逻辑1和逻辑0。它们不是数字符号,而是代表两种相反的逻辑状态。逻辑代数所表示的是逻辑关系,不是数量关系,这时它与普通代数本质上的区别。
在逻辑代数中只有逻辑乘(与运算)、逻辑加(或运算)和求反(非运算)三种基本运算。根据这三种基本运算可以推导出逻辑运算的一些法则,就是下面列出的逻辑代数运算法则。
1、逻辑代数运算法则
【基本运算法则】
(1) 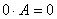
(2) 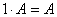
(3) 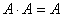
(4) 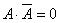
(5) 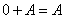
(6) 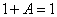
(7) 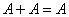
(8) 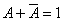
(9) 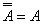
【交换律】
(10)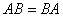
(11)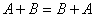
【结合律】
(12)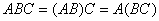
(13)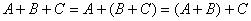
【分配律】
(14)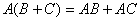
(15)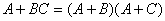
证: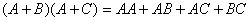
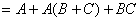
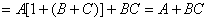
【吸收律】
(16) 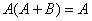
证: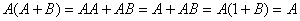
(17)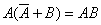
(18)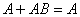
(19)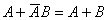
证: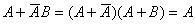
(20)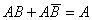
(21)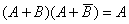
【反演律(摩根定律)】
(22)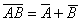
证:
|
|
|
|
|
|
|
|
0 1 0 1 |
0 0 1 1 |
1 0 1 0 |
1 1 0 0 |
1 1 1 0 |
1 1 1 0 |
(23)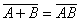
证:
|
|
|
|
|
|
|
|
0 1 0 1 |
0 0 1 1 |
1 0 1 0 |
1 1 0 0 |
1 0 0 0 |
1 0 0 0 |
2、逻辑函数的化简
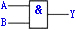
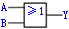
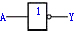
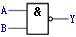
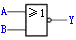
为了便于比较,今将五种常用的逻辑门电路列于表中。可以将这些基本逻辑门电路组合起来,构成组合逻辑电路,以实现各种逻辑功能。
|
逻辑门 |
与 |
或 |
非 |
与非 |
或非 | |
|
逻辑符号 |
|
|
|
|
| |
|
逻辑式 输入逻辑变量 |
|
|
|
|
| |
|
A |
B |
Y |
Y |
Y |
Y |
Y |
|
0 0 1 1 |
0 1 0 1 |
0 0 0 1 |
0 1 1 1 |
1 1 0 0 |
1 1 1 0 |
1 0 0 0 |
表所列的各种逻辑式中,A和B是输入变量,Y是输出变量;字母上面无反号的称为原变量,有反号的称为反变量。这几个式子分别表达了相应的与、或、非、与非和或非逻辑关系。输出变量Y也就是输入变量A和B的逻辑函数。逻辑函数常用逻辑状态表、逻辑式和逻辑图(也称逻辑电路)3种方法表示;它们之间可以相互转换。有时表示逻辑函数的逻辑式较为复杂,可进行化简,这就可以少用元件,可靠性也因而提高。
例1、应用逻辑代数运算法则化简下列逻辑式:
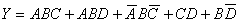
解:
简化得
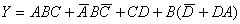
由法则(19)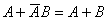 得
得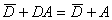 。所以
。所以
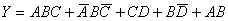
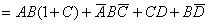
由法则(6)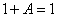 得
得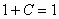 ,所以
,所以
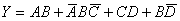
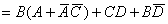
由法则(19)得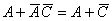 ,所以
,所以
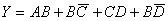
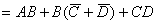
由法则(22)得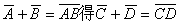 ,所以
,所以
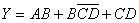
由法则(19)得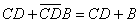 ,所以
,所以
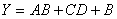
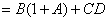
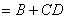
例2、试证明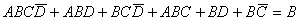
证:
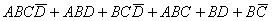
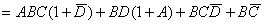
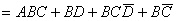
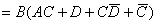 (因
(因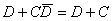 )
)