1．不考虑线圈电阻及漏磁通的电路模型
线圈中的电流（称为励磁电流）除了含有仅产生磁通而不消耗有功功率的磁化电流外，还含有补
偿铁损的电流。
如果用等效正弦量代替，则各电流相量间的关系为
（1）
其中
为补偿铁损的电流。因此，不考虑线圈电阻及漏磁通，线圈可用电导与感纳的并联组合作为电路模型，如图1（a）所示，相量图如图7.16（b）所示。
也可等效变换为R0与X0串联模型，如图1（c）所示。
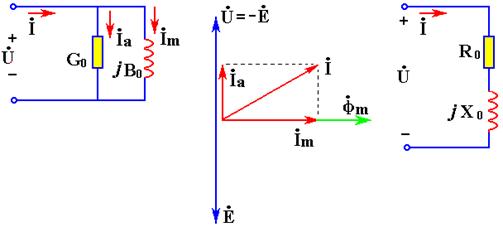
（a） （b） （c）
图1 不考虑线圈电阻及漏磁通的电路模型及相量图
例1 电压Us = 220V的工频正弦电压源接到一匝数N = 100的铁芯线圈上，测得线圈的电流I = 4A ，功率P = 100W 。不计线圈电阻及漏磁通，试求铁芯线圈主磁通的最大值、串联电路模型的Z0 和并联电路模型的Y0 。
解 由式（1）得
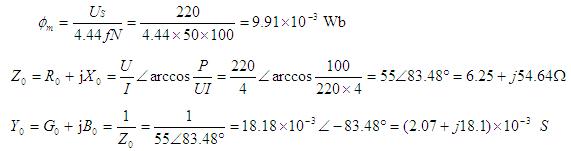
2.考虑线圈电阻及漏磁通的电路模型
考虑线圈电阻的影响,这使得铁芯线圈的总功率为
（2）
反映漏磁通φs用漏磁电感表示:
可得铁芯线圈的相量图和电路模型如图2所示。
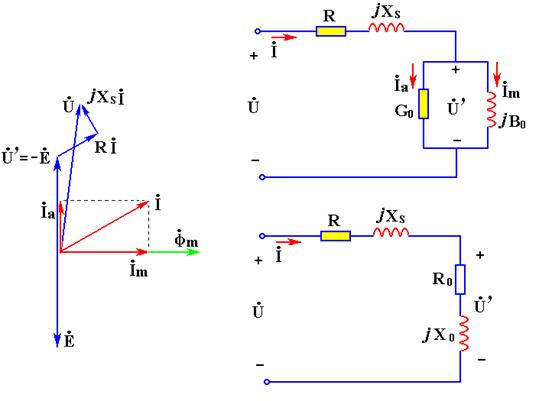
（a）相量图； （b）并联模型； （c）串联模型
图2 考虑线圈电阻及漏磁通的电路模型
例2 电阻R = 0.2Ω，漏抗Xs = 0.3Ω的铁芯线圈接在U = 100V的正弦电压下，测得电流I =10A，有功功率P = 120W 。试求铁损PFe 、主磁通产生的感应电动势E及磁化电流Im，并作相量图。
解 线圈铜损为
铁损为
功率因数为
° 
如设
则
感应电动势为
磁化电流为
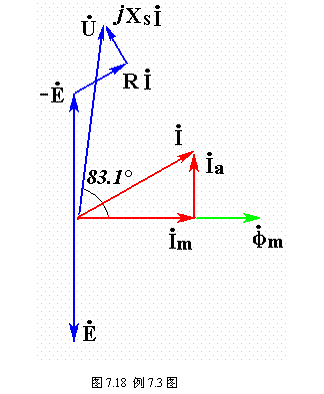
相量图如图7.18所示。
3.伏安特性和等效电感
① 伏安特性：
铁芯线圈电压有效值与电流有效值之间的关系曲线，即U – I曲线称为铁芯线圈的伏安特性，该曲线与铁芯材料的基本磁化曲线相似，如图图3所示。
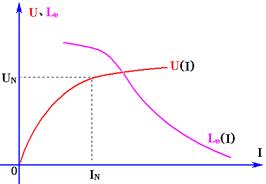
图3 交流铁芯线圈的伏安特性与等效电感
② 等效电感：
忽略铁芯线圈的功率损耗，就可以用一个电感作为它的电路模型，称之为等效电感。
Le是非线性的，如图7.19所示。Le的最大值在U – I曲线的膝点处，在电压较低时Le近似于常量。