发生在放大电路中的自激振荡是有害的，必须设法消除。最简单的方法是减小反馈深度，如减小反馈系数
，但这又不利于改善放大电路的其他性能。为了解决这个矛盾，常采用频率补偿的办法（或称相位补偿法）。其指导思想是：在反馈环路内增加一些含电抗元件的电路，从而改变
的频率特性，破坏自激振荡的条件，例如使
，则自激振荡必然被消除。<?XML:NAMESPACE PREFIX = O />
频率补偿的形式很多，下面先介绍滞后补偿。设反馈网络为纯电阻网络。
滞后补偿是在反馈环内的基本放大电路中插入一个含有电容C的电路，使开环增益
的相位滞后，达到稳定负反馈放大电路的目的。
1. 电容滞后补偿
|
|
|
(a) |
|
|
|
(b) |
|
|
|
(c) |
|
图1 |
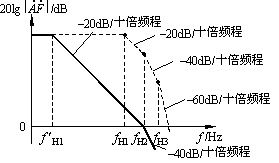
由前面的分析及稳定裕度的要求可知，若 
的幅频特性曲线在0dB以上只有一个转折频率（拐点），且下降斜率为–20dB/十倍频程，则属于只有一个RC回路的频率响应，最大相移不超过–90°。若在它的第二个转折频率（拐点）处对应的
，且此处的最大相移为–135°(有45°的相位裕度)，这样的负反馈放大电路是稳定的，因此电容滞后补偿即按此思路进行。
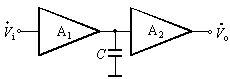
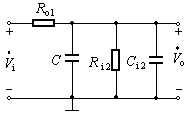
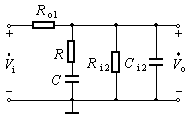
这种补偿是将电容并接在基本放大电路中时间常数最大的回路里，即前级的输出电阻和后级的输入电阻都比较大的地方，如图1（a）所示。图1（b）是该补偿电路的高频等效电路。其中Ro1为前级的输出电阻，Ri2为后级的输入电阻，Ci2为后级的输入电容。未加电容前该反馈放大电路环路增益
的幅频特性如图1(c)中的虚线所示，此时的上限频率为
加补偿电容C后的上限频率为
只要选择合适的电容C，使得修改后的幅频特性曲线上，以–20dB/十倍频程斜率下降的这一段曲线与横轴的交点刚好在第二个转折频率fH2处，此处的
，如图1（c）中的实线所示，此时的（φa+φf）趋于–135°，即
，且保证φm≥45°，所以负反馈放大电路一定不会产生自激振荡。
2. RC滞后补偿
|
|
|
(a) |
|
|
|
(b) |
|
|
|
(c) |
|
|
|
(d) |
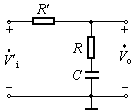
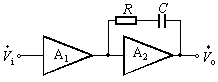
电容滞后补偿虽然可以消除自激振荡，但使通频带变得太窄。采用RC滞后补偿不仅可以消除自激振荡，而且可使带宽得到一定的改善。具体电路如图2（a）所示，图（b）是它的高频等效电路。通常应选择<?XML:NAMESPACE PREFIX = V />
，C≥Ci2，所以可将图（b）简化为图（c）的形式，其中
， 
它的电压传输函数为
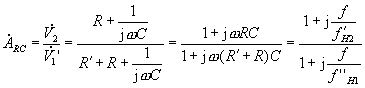
式中 
= 
，
设未加RC补偿电路前，反馈放大电路的环路增益的表达方式为
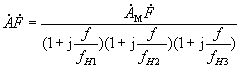
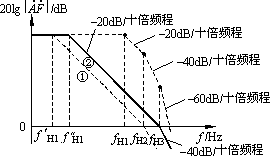
其幅频特性如图2（d）中虚线所示。
只要选择合适的RC参数，使
，那么加入RC补偿电路后，环路增益的表达式即变为
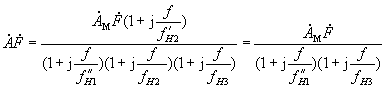
此式说明，加入RC补偿电路后，环路增益的幅频特性曲线上只有两个转折频率，而且如果
的选择，使得修改后的幅频特性曲线上以–20dB/十倍频程斜率下降的这一段曲线与横轴的交点刚好在fH3处，此处的
，如图2（d）中实线②所示，此时的（
）趋于–135°。所以加入RC滞后补偿的负反馈放大电路一定不会产生自激振荡。
图2(d)的虚线①是采用电容滞后补偿的幅频特性，很显然，RC滞后补偿后的上限频率向右移了，说明带宽增加了。
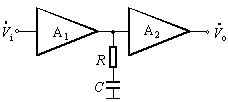
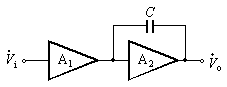
前两种滞后补偿电路中所需电容、电阻都较大，在集成电路中难以实现。通常可以利用密勒效应，将补偿电容等元件跨接于放大电路中，如图3（a）、（b）所示，这样用较小的电容（几皮法~几十皮法）同样可以获得满意的补偿效果。
|
|
|
|
(a) |
(b) |
