1 .按照傅里叶级数展开法,任何一个满足狄里赫利 (Dirichlet) 条件的非正弦周期信号 ( 函数 ) 都可以分解为一个恒定分量与无穷多个频率为非正弦周期信号频率的整数倍、不同幅值的正弦分量的和,如图所示,即 周期函数
![]()
![]() ,称为直流分量
,称为直流分量
![]() ,
,
![]()
![]() ,称为第 K 次谐波分量的振幅。
,称为第 K 次谐波分量的振幅。
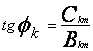 ,称为第 K 次谐波分量的初相角。
,称为第 K 次谐波分量的初相角。
例 : 周期性方波的分解: ![]() ,
,
分解波形如图所示。
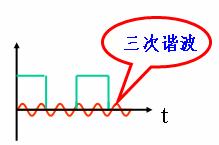
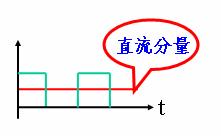
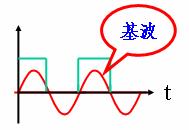
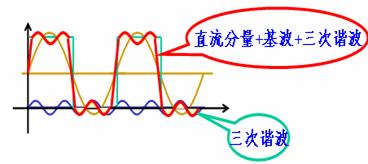
图 方波波形的分解
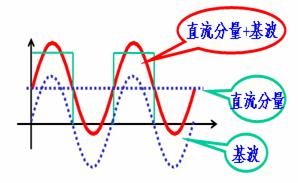
例 : 锯齿波信号的分解
![]()
例 : 三角波信号的分解
![]()
1 .按照傅里叶级数展开法,任何一个满足狄里赫利 (Dirichlet) 条件的非正弦周期信号 ( 函数 ) 都可以分解为一个恒定分量与无穷多个频率为非正弦周期信号频率的整数倍、不同幅值的正弦分量的和,如图所示,即 周期函数
![]()
![]() ,称为直流分量
,称为直流分量
![]() ,
,
![]()
![]() ,称为第 K 次谐波分量的振幅。
,称为第 K 次谐波分量的振幅。
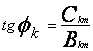 ,称为第 K 次谐波分量的初相角。
,称为第 K 次谐波分量的初相角。
例 : 周期性方波的分解: ![]() ,
,
分解波形如图所示。




图 方波波形的分解

例 : 锯齿波信号的分解
![]()
例 : 三角波信号的分解
![]()
下一篇三相负载的功率因数