一阶电路根据KVL和KCL建立微分方程，利用高等数学求解微分方程的方法，可求得一阶RL电路和RC电路的通解为：
其中三个要素分别为所求变量的初始值
、特解
和时间常数
。用微分方程分析方法关键是求解变量的三个要素。
对于一阶电路，求解电路中任一响应随时间的变化规律，都可以利用三要素法。
而对于一阶RL电路，无任需要求解哪个变量，都可以首先求解电感电流随时间的变化规律，别的变量随时间的变化可以根据所求的电感电流、已知的电路结构和参数来求解。而电感电流的独立初始值可根据换路定则得出。
而对于一阶RC电路，无任需要求解哪个变量，都可以首先求解电容电压随时间的变化规律，别的变量随时间的变化可以根据所求的电容电压、已知的电路结构和参数来求解。而电容电压的独立初始值可根据换路定则得出。
三要素法数学表达式中，
随时间变化而不断减小，因而称为动态电路的暂态分量（自由分量）。特解主要由外加激励决定，因此它为动态电路的强制分量。当外加激励为直流或交流时，特解为稳态分量。
<?xml:namespace prefix = o />
2、一阶电路的全响应
1）全响应的定义：在非零状态的动态电路中，外加激励所引起的电路响应。
2）全响应解的组成
在图1电路中，电阻、电容以及电压源全部为已知参数，开关S在t=0时刻从位置1合到位置2，开关移动之前电路处于稳态，求换路后的电容电压
。
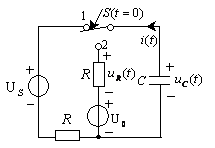
图1一阶电路的全响应
根据一阶电路的三要素法得：
，即全响应=强制分量（稳态解）+自由分量（暂态解）；
或全响应表达为：
，即表示全响应=零输入响应+零状态响应。
这三种情况电容电压随时间变化情况如图2所示。
图2电容电容随时间的变化
当
时，外加激励换路后对电容充电；当
时，换路后，电路瞬间进入稳态，电路没有过渡过程；当
时，换路后电容对外电路放电。