你家里一定有这样的电路:门边一个开关,床头一个开关,在哪个位置都可以控制灯的亮灭。它的原理图如下:
(图1)

2个开关控制一盏灯电路
这个电路原理简单,我们就不分析了。那么,能否用三个开关控制一盏灯呢?下图的电路可以完成这样的功能:
(图2)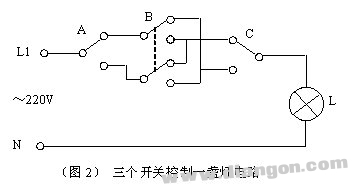
三个开关控制一盏灯电路
其中的开关B是一个双刀双掷开关。我们可以用数字逻辑电路的分析方法来分析它的工作原理:
A、B、C三个开关,每个都有上、下两种位置,3个开关共有8种位置组合。假设开关拔为“0”,拔下为“1”,灯泡L灭为“0”,亮为“1”,在上图所示的电路中,A、B、C为“000”组合,灯泡是灭的(L=0),如果拔动了其中一个开关,例如C,则变为“001”组合,灯泡亮(L=1)……这样逐一分析8种开关的位置组合,可得到L与A、B、C的逻辑关系真值表:
表1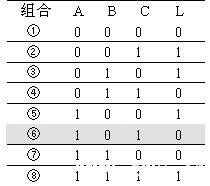
三个开关控制一盏灯的真值表
从表中可看出无论三个开关处于哪一种状态,只要改变一个开关的位置,就能改变灯泡的亮灭。例如在组合⑥,L是灭的,若改变开关A,变为001(组合②),则灯亮;改变B、C,同样可以使灯泡变亮。这样就实现了3个开关控制一盏灯的目的。
按上述的思路,可以设计出4个开关控制一盏灯的电路。4个开关控制一盏灯,用简单的电气线路来实现将会很困难,但用电子线路来实现就很容易了。事实上这是一道非常有趣的数字逻辑电路设计题,解答方法如下:四个开关A、B、C、D,每个开关有2个位置,则有16种位置组合;假设0000时L为0,掀动一个开关后L应该为1;再掀动一个开关后L又为0……这样可得到真值表如表2: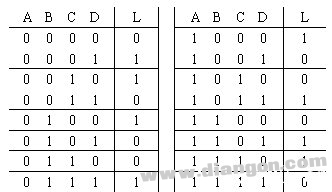
根据真值表可写出逻辑表达式:
L=ABCD+ABCD+ABCD+ABCD+ABCD+ABCD+ABCD+ABCD
这个式子,如果用卡诺图法来化简,结果会发现它已经是一个“最简与或式”,但用代数法可以化简为“异或式”:
L=(A+B)+(C+D)
这样,我们可以用三个“异或门”来实现它。逻辑图如(图3):
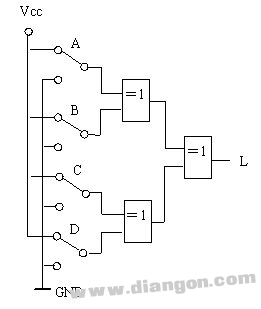
4个开关控制一盏灯路逻辑图
TTL系列的数字集成电路中的74LS86就是一个“四异或门”,使用5V直流电源,可以做成如下(图4)
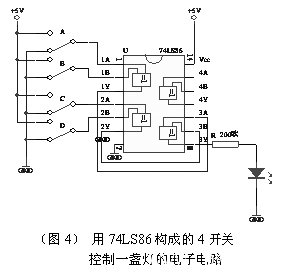
所示的模拟装置:
这还只是一个电子装置。如果加上稳压电源电路,用输出去触发可控硅(或控制继电器等),装在220V源上,那么你就可以在四层楼的任一层楼梯口,随意地控制梯灯的亮灭!
