数控车床与普通车床相比具有适应性强,加工精度高,生产效率高,能完成复杂型面的加工等特点。随着新产品的开发,其形状越来越复杂,精度要求也越来越高,无疑要充分发挥数控车床的优点。圆弧加工就体现了数控车床的优点。但是,在实际加工大圆弧时,由于加工工艺的选择不当或缺少辅助计算工具常常出现编程困难,重者出现异常加工误差。对此引起了我的注意,通过长期的试切实验,证明应用下面方法在圆弧编程中思路简单,加工出的零件精度高。下面我以几种常见零件为例与大家一起讨论。
一、圆弧分层切削法
1) 圆弧始点、终点均不变,只改变半径R
如图1所示,在零件加工一个凸圆弧,根据过两点作圆弧,半径越小曲率越大的原则,因此在切削凸圆弧时,可以固定始点和终点把半径R由小逐渐变大至规定尺寸。但要注意,圆弧半径最小不得小于成品圆弧弦长的一半。
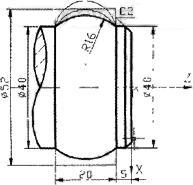
图1
N10 G01 X40 Z-5 F0.3;
N20 G03 X40 Z-25 R10.2 F0.2;
N30 G00 X53;
N40 Z-5;
N50 G01 X40 F0.3;
N60 G03 X40 Z-25 R12 F0.2;
N70 G00 X53;
N80 Z-5;
N90 G01 X40 F0.3;
N100 G03 X40 Z-25 R16 F0.1 :
2) 圆弧始点、终点坐标变化,半径R不变
如图2所示,在零件上加工一个凹圆弧,为了合理分配吃刀量,保证加工质量,采用等半径圆弧递进切削,编程思路简单。
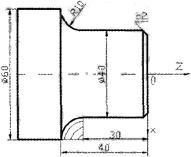
图2
N10 G01 X54 Z-30 F0 .3;
N20 G02 X60 Z-33 R10 F0 .2;
N30 G00 X54 Z-30;
N40 G01 X48 F0.3 ;
N50 G02 X60 Z-36 R10 F0.2;
N60 G00 X48 Z-30;
N70 G01 X42 F0.3 ;
N80 G02 X60 Z-39 R10 F0.2;
N90 G00 X42 Z-30;
N100 G01 X40 F0.3;
N110 G02 X60 Z-40 R10 F0.1;
3) 圆弧始点、终点坐标,半径R均变化
如图3所示,在零件一端加工一个半球,在该种情况下,走刀轨迹的半径R等于上次走刀半径R与Z(或X)方向的变化量∆Z(∆X)之差。
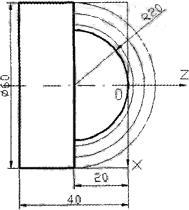
图3
N10 G01 X0 Z10 F0.3;
N20 G03 X60 Z-20 R30 F0.2 ;
N30 G00 Z6;
N40 X0;
N50 G03 X60 Z-20 R26 F0.2;
N60 G00 Z2;
N70 X0;
N80 G03 X60 Z-20 R22 F0.2 ,
N90 G00 Z0;
N100 X0;
N110 G03 X60 Z-20 R20 F0.1;
二、先锥后圆弧法
该方法是先把过多的切削余量用车锥的方法切除掉,最后一刀走圆弧的路线切削圆弧成型,如图4所示。
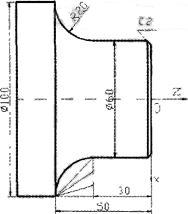
图4
N10 G01 X102 Z-30 F0.3;
N20 G90 X100 Z-50 I-5 F0.2;
N30 I-10;
N40 I-15;
N50 I-20;
N60 G01 X60 Z-30 F0.3;
N70 G02 X100 Z-50 R20 F0.1;
当是凸圆弧时,可根据几何知识算出ab段的长度,然后再车锥,最后车弧,如图5所示。
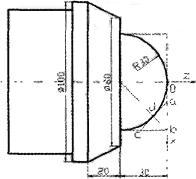
图5
db=1.414R+R=0.414R
ab=1.414*db=0.585R
留取一部分精加工余量,则ab取0.5R,
ab=bc
根据1中的方法先加工出锥形,然后再精车圆弧。
三、结束语
在数控加工中,往往机床操作者也是零件切削程序的编制者,这就要求编制的程序工艺简单,调整方便,加工精度高等。在操作现场没有CAD制图软件、计算机等辅助计算工具时,采用上述方法编程切削圆弧可大大减少计算量。思路简单,工艺得体,延长刀具的使用寿命,加工出来的零件精度高,为圆弧类零件的加工带来方便。
