在变压器设计时,其空载时的电感量足够大,其感抗也大,而电阻指铜阻和铁阻,铜阻是指绕变压器铜导线的电阻,应该很小,铁阻是铁芯变压器的磁滞损耗,铁阻与铁芯的磁滞回线面积成正比,好的变压器尽量选择磁滞回线面积小的铁芯,这部分的电阻也很小。
在研究变压器的运行问题时,希望有一个既能正确反映变压器内部电磁关系,又便于工程计算的等效电路,来代替具有电路、磁路和电磁感应联系的实际变压器。下面从变压器的基本方程出发,导出此等效电路。
绕组归算为建立等效电路,除了需要把一次和二次侧漏磁通的效果作为漏抗压降,主磁通和铁心线圈的效果作为激磁阻抗来处理外,还需要进行绕组归算,通常是把二次绕组归算到一次绕组,也就是假想把二次绕组的匝数变换成一次绕组的匝数,而不改变一次和二次绕组原有的电磁关系。
从磁动势平衡关系可知,二次电流对一次侧的影响是通过二次磁动势N2I2起作用,所以只要归算前后二次绕组的磁动势保持不变,一次绕组将从电网吸收同样大小的功率和电流,并有同样大小的功率传递给二次绕组。
归算后.二次侧各物理量的数值称为归算值,用原物理量的符号加“′”来表示。设二次绕组电流和电动势的归算值为![]() ′和
′和![]() ′,根据归算前、后二次绕组磁动势不变的原则,可得
′,根据归算前、后二次绕组磁动势不变的原则,可得![]()
由此可得二次电流的归算值![]() ′为
′为

由于归算前、后二次绕组的磁动势未变,因此铁心中的主磁通将保持不变;这样,根据感应电动势与匝数成正比这一关系,便得
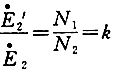
即二次绕组感应电动势的归算值![]() ′为
′为
![]()
再把二次绕组的电压方程(式(2—22)中的第二式)乘以电压比k,可得
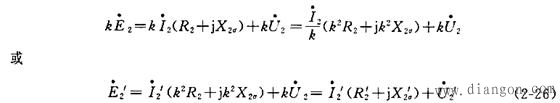
式中,R2′和X2σ′分别为二次绕组电阻和漏抗的归算值,R2′=k2R2,X2σ′= k2X2σ;![]() ′则是二次电压的归算值,
′则是二次电压的归算值,![]() ′=k
′=k![]() 。
。
综上所述可见,二次绕组归算到一次绕组时,电动势和电压应乘以k倍,电流乘以1/k倍,阻抗乘以k2倍。不难证明,这样做的结果,归算前、后二次绕组内的功率和损耗均将保持不变。例如,传递到二次绕组的复功率为
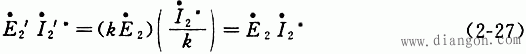
式中,*号表示复数的共轭值。二次绕组的电阻损耗和漏磁场内的无功功率为
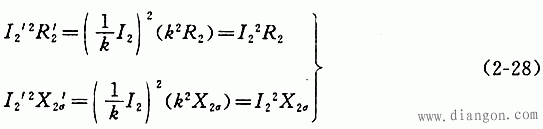
负载的复功率为
![]()
即用归算前、后的量算出的值为相同.因此,所谓归算,实质是在功率和磁动势保持为不变量的条件下,对绕组的电压、电流所进行的一种线性变换。
归算后,变压器的基本方程变为
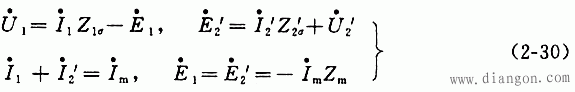
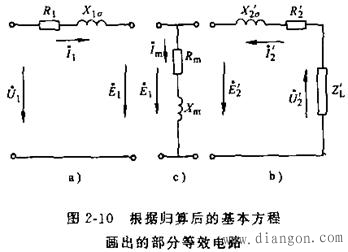 T形等效电路 归算以后,一次和二次绕组的匝数变成相同,故电动势
T形等效电路 归算以后,一次和二次绕组的匝数变成相同,故电动势![]() =
=![]() ′,一次和二次绕组的磁动势方程也变成等效的电流关系
′,一次和二次绕组的磁动势方程也变成等效的电流关系![]() ′=
′=![]() ,由此即可导出变压器的等效电路。
,由此即可导出变压器的等效电路。
根据式(2—30)中的第一式和第二式,可画出一次和二次绕组的等效电路,如
图2—lOa和b所示;根据第四式可画出激磁部分的等效电路,如图2--10c所示。然后根据![]() ′和
′和![]() ′=
′=![]() 两式,把这三个电路连接在一起,即可得到变压器的T形等效电路,如图2—11所示。
两式,把这三个电路连接在一起,即可得到变压器的T形等效电路,如图2—11所示。
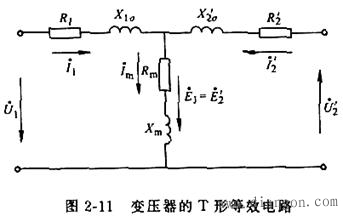 工程上常用等效电路来分析、计算各种实际运行问题。应当指出,利用归算到一次侧的等效电路算出的一次绕组各量,均为变压器的实际值;二次绕组中各量则为归算值,欲得其实际值,对电流应乘以k(
工程上常用等效电路来分析、计算各种实际运行问题。应当指出,利用归算到一次侧的等效电路算出的一次绕组各量,均为变压器的实际值;二次绕组中各量则为归算值,欲得其实际值,对电流应乘以k(![]() ′),对电压应除以k(即
′),对电压应除以k(即![]() ′/k)。
′/k)。
亦可以把一次侧各量归算到二次侧,以得到归算到二次侧的T型等效电路。一次侧各量归算到二次侧时,电流应乘以k,电压除以k,阻抗乘以l/k2。
近似和简化等效电路 T形等效电路属于复联电路,计算起来比较繁复。对于一般的电力变压器,额定负载时一次绕组的漏阻抗压降I1NZ1σ仅占额定电压的百分之几,加上激磁电流Im又远小于额定电流I1N,因此把T形等效电路中的激磁分支从电路的中间移到电源端,对变压器的运行计算不会带来明显的误差。这样,就可得到图2—12a所示近似等效电路。
若进一步忽略激磁电流(即把激磁分支断开).则等效电路将简化成一串联电路,如图2—12b所示,此电路就称为简化等效电路。在简化等效电路中,变压器的等效阻抗表现为一串联阻抗Zk,Zk称为等效漏阻抗,
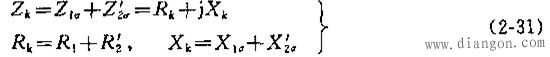
下面将看到,等效漏阻抗Zk可用短路试验测出,故Zk亦称为短路阻抗;Rk和Xk则称为短路电阻和短路电抗。用简化等效电路来计算实际问题十分简便,在多数情况下其精度已能满足工程要求。
