1. 动态网络的过渡过程是十分短暂的单次变化过程。要用普通示波器观察过渡过程和测量有关的参数,就必须使这种单次变化的过程重复出现。为此,我们利用信号发生器输出的方波来模拟阶跃激励信号,即利用方波输出的上升沿作为零状态响应的正阶跃激励信号;利用方波的下降沿作为零输入响应的负阶跃激励信号。只要选择方波的重复周期远大于电路的时间常数τ,那么电路在这样的方波序列脉冲信号的激励下,它的响应就和直流电接通与断开的过渡过程是基本相同的。
2. 图1(b)所示的 RC 一阶电路的零输入响应和零状态响应分别按指数规律衰减和增长,其变化的快慢决定于电路的时间常数τ。
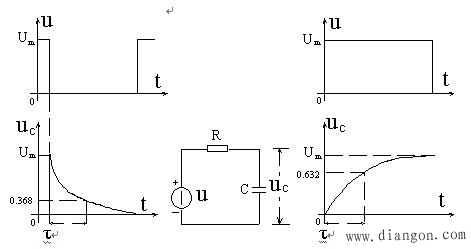
(a) 零输入响应 (b) RC一阶电路 (c) 零状态响应
图1
3. 时间常数τ的测定方法:
用示波器测量零输入响应的波形如图1(a)所示。
根据一阶微分方程的求解得知uc=Ume-t/RC=Ume-t/τ。当t=τ时,Uc(τ)=0.368Um。此时所对应的时间就等于τ。亦可用零状态响应波形增加到0.632Um所对应的时间测得,如图1(c)所示。
4. 微分电路和积分电路是RC一阶电路中较典型的电路,它对电路元件参数和输入信号的周期有着特定的要求。一个简单的 RC串联电路,在方波序列脉冲的重复激励下,当满足τ=RC<< T/2 时(T为方波脉冲的重复周期),且由R两端的电压作为响应输出,则该电路就是一个微分电路。因为此时电路的输出信号电压与输入信号电压的微分成正比。如图2(a)所示。利用微分电路可以将方波转变成尖脉冲。
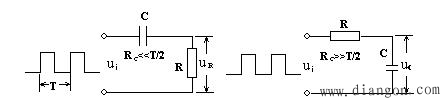
(a)微分电路 (b) 积分电路
图2
若将图2(a)中的R与C位置调换一下,如图2(b)所示,由 C两端的电压作为响应输出,且当电路的参数满足τ=RC>> T/2,则该RC电路称为积分电路。因为此时电路的输出信号电压与输入信号电压的积分成正比。利用积分电路可以将方波转变成三角波。
从输入输出波形来看,上述两个电路均起着波形变换的作用,请在测试过程中仔细观察与记录。
