机械性能参数对系统性能的影响

 机械传动系统的性能与系统本身的阻尼比ξ、固有频率ωn有关。ωn、ξ又与机械系统的结构参数密切相关。因此,机械系统的结构参数对伺服系统的性能有很大影响。 一般的机械系统均可简化为二阶系统,系统中阻尼的影响可以由二阶系统单位阶跃响应曲线来说明。由图2-13可知,阻尼比不同的系统,其时间响应特性也不同。 （1）当阻尼比ξ＝0时,系统处于等幅持续振荡状态,因此系统不能无阻尼。 （2） 当ξ≥ 1时,系统为临界阻尼或过阻尼系统。此时,过渡过程无振荡,但响应时间较长。 （3） 当0<ξ<1时,系统为欠阻尼系统。此时,系统在过渡过程中处于减幅振荡状态,其幅值衰减的快慢,取决于衰减系数ξωn。在ωn确定以后, ξ愈小,其振荡愈剧烈,过渡过程越长。相反,ξ越大,则振荡越小,过渡过程越平稳,系统稳定性越好,但响应时间较长,系统灵敏度降低。

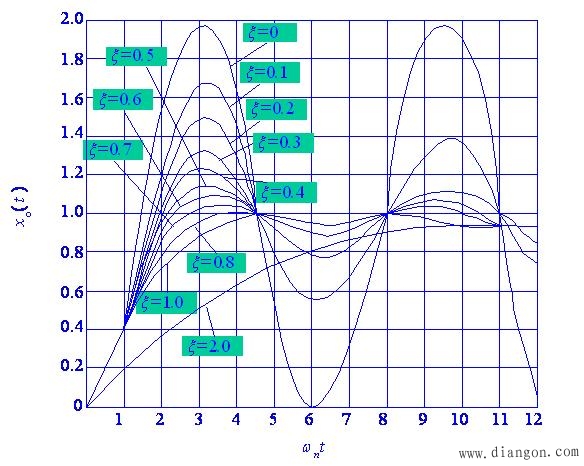
图2-13 二阶系统单位阶跃响应曲线
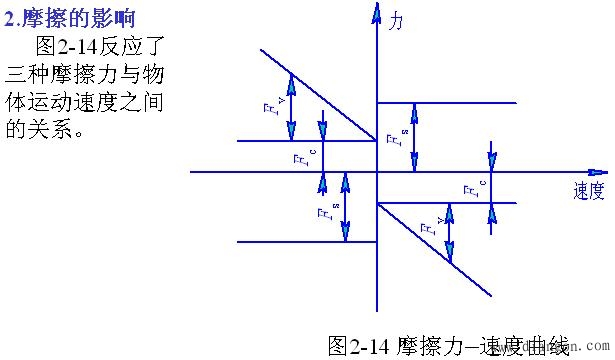在图2-15所示的机械系统中,设系统的弹簧刚度为K。如果系统开始处于静止状态，当输入轴以一定的角速度转动时,由于静摩擦力矩T的作用,在θi≤ 范围内,输出轴将不会运动, θi值即为静摩擦引起的传动死区。在传动死区内,系统将在一段时间内对输入信号无响应,从而造成误差。 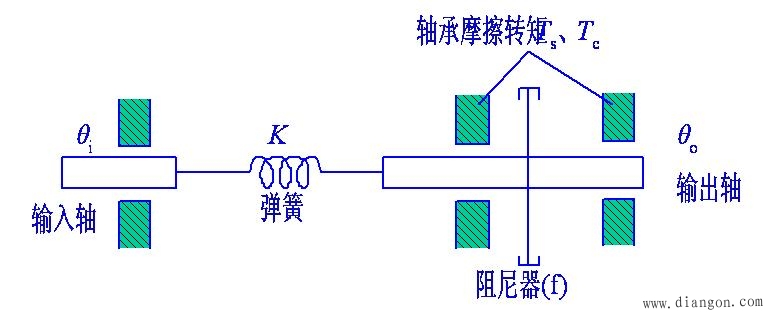图 2-15 力传递与弹性变形示意图
当输入轴以恒速Ω继续运动,在θi>|Ts/K|后,输出轴也以恒速Ω运动,但始终滞后输入轴一个角度θss,若粘性摩擦系数为f,则有
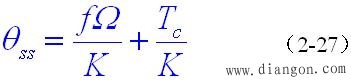式中: fΩ/K是粘性摩擦引起的动态滞后；Tc/K是库仑摩擦所引起的动态滞后；θss为系统的稳态误差。 此外,适当的增加系统的惯量J和粘性摩擦系数f也有利于改善低速爬行现象。但惯量增加将引起伺服系统响应性能的降低,增加粘性摩擦系数f也会增加系统的稳态误差,故设计时必须权衡利弊,妥善处理。 3. 弹性变形的影响 由式(2-25)、(2-26)知,其固有频率与系统的阻尼、惯量、摩擦、弹性变形等结构因素有关。当机械系统的固有频率接近或落入伺服系统带宽之中时,系统将产生谐振而无法工作。因此为避免机械系统由于弹性变形而使整个伺服系统发生结构谐振,一般要求系统的固有频率ωn要远远高于伺服系统的工作频率。 4. 惯量的影响 由式(2-26)可以看出,惯量大,ξ值将减小,从而使系统的振荡增强,稳定性下降； 由式(2-25)可知,惯量大,会使系统的固有频率下降,容易产生谐振,因而限制了伺服带宽,影响了伺服精度和响应速度。 5.传动间隙对系统性能的影响 图2-16所示为一典型旋转工作台伺服系统框图。图中所用齿轮根据不同的要求有不同的用途,有的用于传递信息（G1、G3）,有的用于传递动力（G2、G4）；有的在系统闭环之内（G2、G3）,有的在系统闭环之外（G1、G4）。由于它们在系统中的位置不同,其齿隙的影响也不同。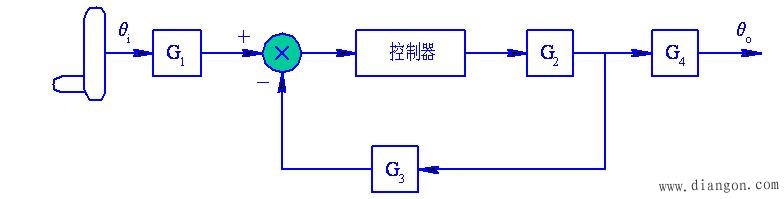 图2-16 典型转台伺服系统框图 (1) 闭环之外的齿轮G1、G4的齿隙对系统稳定性无影响,但影响伺服精度。 (2) 闭环之内传递动力的齿轮G2的齿隙对系统静态精度无影响,这是因为控制系统有自动校正作用。 (3) 反馈回路上数据传递齿轮G3的齿隙既影响稳定性,又影响精度。