仅含一个储能元件或可等效为一个储能元件的线性电路 , 且由一阶微分方程描述,称为 一阶线性电路。 在直流电源激励的情况下,一阶线性电路微分方程解的通用表达式:

式中 , f(t) 代表一阶电路中任一电压、电流函数

利用求三要素的方法求解暂态过程,称为 三要素法 。 一阶电路都可以应用三要素法求解, 在求得 、和 t 的基础上 , 可直接写出电路的响应 ( 电压或电流 ) 。
电路响应的变化曲线
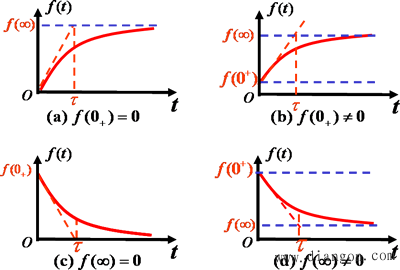
三要素法求解暂态过程的要点
(1) 求初始值、稳态值、时间常数;
(2) 将求得的三要素结果代入暂态过程通用表达式;
(3) 画出暂态电路电压、电流随时间变化的曲线。
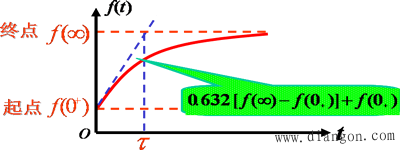
响应中 “ 三要素 ” 的确定
(1) 稳态值f(∞) 的计算
求换路后电路中的电压和电流 , 其中 电容 C 视为开路 , 电感 L 视为短路,即求解直流电阻性电路中的电压和电流。
(2) 初始值f(0+)的计算

(3) 时间常数 t 的计算
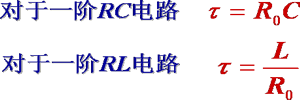
注意:
1) 对于简单的一阶电路 , R 0 = R ;
2) 对于较复杂的一阶电路, R 0 为换路后的电路除去电源和储能元件后,在储能元件两端所求得的无源二端网络的等效电阻。

