一、精度设计中的基本概念
1.精度与误差
精度是指实际参数和理想参数的符合程度
误差是指实际参数与理想参数的偏离程度
2.误差的分类
(1)根据误差的性质
随机误差、系统误差、粗大误差
(2)按误差来源
原理误差、制造误差、运行误差
二、机电一体化系统的精度分配
(一)产品精度分配依据和步骤
1.精度分配依据
2.精度分配步骤
(二)误差分配方法
产品总误差△包括总系统误差△s和总随机误差△r,即△=△s+ △r
1.总系统误差的分配
产品设计时,一般要求总系统误差△s不大于产品允许的总误差△的三分之一,即△s≤1/3 △
2.随机误差的分配
总随机误差△ r = △- △s
随机误差的分配方法有:等作用原则和不等作用原则
等作用分配原则:
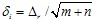
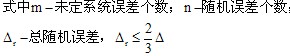
不等作用分配原则:

3.公差调整
三个方面公差评定等级:经济公差极限、生产公差极限、技术公差极限
4.误差补偿
误差补偿法是在产品设计时采取误差补偿措施减小或消除误差的影响。零部件参数对品精度的影响是误差值和误差传递系数,因而有三种补偿方法:
误差值补偿:分级补偿、连续补偿、自动补偿
误差传递系数补偿
综合补偿
三.误差的综合
1.随机误差的合成
设有n个随机原始标准偏差σ1, σ2,… σn,根据方差运算规则,其合成的总随机误差标准偏差σ为

合成后总误差(总随机不确定度)的极限误差△r为
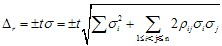
式中t-总误差分布的对应致信系数,它与置信概率及其对应的随机误差分布有关。

2.系统误差的合成
(1)已定系统误差的合成-代数和法
设有r个已知系统误差,则已定系统误差△s为
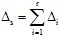
(2)未定系统误差的合成
绝对和法(最大最小法)-对总误差的估计偏高
若各单项未定系统误差的不确定度为ei,i=1~n,则总误差的不确定度△s按绝 对值相加
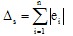
方和根法-计算结果略低于实际的总误差
设有m个未定的系统误差ei,则总误差的不确定度△s为
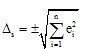
广义方和根法-适用于任何概率分布的误差合成
总合成误差△s为

3.不同性质误差的合成
(1)已定系统误差与随机误差的合成
设各单项原始误差中,有r个已定系统误差△i ,n个随机误差δi,则其合成误差△为
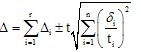
(2)随机误差、已定系统误差与未定系统误差的合成
设各单项原始误差中,有r个已定系统误差△i ,m个未定系统误差ei,n个随机误差δi,则其合成误差△有三种情况:
A.若计算一台精密设备的最大极限误差,则未定系统误差的随机性大为减少。此时,未定系统误差可按绝对和法计算,合成误差为
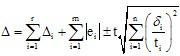
B.若计算一批同类精密设备的合成极限误差,则未定系统误差呈现随机误差性质,应按随机误差的合成方法处理
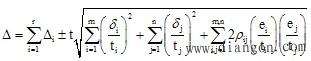
C.若在一批精密设备中,求某台精密设备的总极限误差,则强调未定系统误差的双重性,而它与随机误差和成时,强调系统性质。若按系统误差与随机误差和成方法处理,则合成误差为
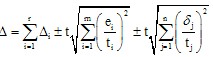
四、实例:数控机床精度分析
数控机床与一般机床比较,影响加工精度的误差源较多,而且有些误差源是数控机床特有的。数控机床的误差源可分为三大类
(一)加工前的误差源
1.编程误差
2.机床的调整误差
3.自动换刀误差
(二)机床本身的误差
1.机床的几何精度误差
2.弹性变形引起的误差
(三)运行时的误差
1.定位误差
2.各种运行速度下的误差
(1)快速运行过程中引起的误差
(2)中速运行过程中引起的误差
(3)缓慢运行过程中引起的误差
通过对数控机床精度分析和研究,可以得到以下结论:
①表面粗糙度、形状和表面相互位置精度基本上是由机床机械部分形成的,它决定于几何精度、刚度、株洲部件的制造精度等。
②沿着X、Y、Z轴的尺寸精度反映了数控机床的特点,它是由机床机械部分和数控系统共同形成的。
③轮廓加工时,要考虑各坐标轴尺寸精度对轮廓加工的不同影响。
④在进给传动的闭环控制系统中,执行机构的位移精度在很大程度上决定于反馈系统测量传感器的分辨率和安装位置。
⑤计算机数控能够系统一般具有校正机床误差和诊断机床及数控系统状态的功能,因此,机床加工精度也与此有很大关系,但可以进行调整来减小它的影响。
