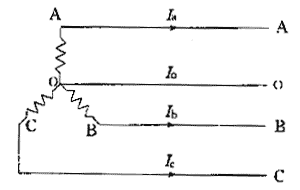
三相四线制结线方式如图1所示。
ΔP1=I2aR+I2bp+I2cR+I2o×2R=(1)
式中R--单位长度线路的电阻值,中性线的截面积通常只有相线的一半,故中性线的单位长度线路的电阻值取2R。
当三相负荷完全平衡时,三相电流Ia=Ib=Ic=Icp,中性线的电流Io=0,这时单位长度线路上的功率损耗为:
ΔP=3I2cpR(2)
如果各相电流不平衡,则中性线中有电流通过,损耗将显著增加。为讨论方便,引入负荷不平衡度β概念:
β=(Imax-Icp)/Icp×100%(3)
式中Imax--负荷最大一相的电流值
Icp--三相负荷完全平衡时的相电流值
下面分三种情况讨论三相负荷不平衡时线损值的增量。
1、一相负荷重,两相负荷轻
假设A相负荷重,B、C相负荷轻,则Ia=(1+β)×Icp,Ib=Ic=(1-β/2)Icp,在三相相位对称的情况下,中性线的电流Io=32βIcp。代入式(1),这时单位长度线路上的功率损耗为:
ΔP1=(1+β)2I2cpR+2(1-β/2)2I2cpR+94β2I2cp×2R=3I2cpR+6β2I2cpR(4)
它与三相负荷平衡时单位长度线路上的功率损耗的比值,称为功率损耗增量系数。其值为K则:
K1=ΔP1ΔP=3I2cpR+6β2I2cpR/3I2cpR=1+2β2(5)
2、一相负荷重,一相负荷轻,第三相的负荷为平均负荷
假设A相负荷重,B相负荷轻,C相负荷为平均值,显然Ia=(1+β)Icp,Ib=(1-β)Icp,Ic=Icp,则在三相相位对称的情况下,中性线的电流 。得出单位长度线路上的功率损耗为:
ΔP2=(1+β)2I2cpR+(1-β)2I2cpR+I2cpR+3β2I2cp×2R=3I2cpR+8β2I2cpR(6)
K2=ΔP2ΔP=3I2cpR+8β2I2cpR3I2cpR=1+8/3β2(7)
3、一相负荷轻,两相负荷重
假设Ia=(1-2β)Icp,Ib=Ic=(1+β)Icp,则在三相相位对称的情况下,中性线的电流Io=3βIcp。这时单位长度线路上的功率损耗为:
ΔP3=(1-2β)2I2cpR+2(1+β)2I2cpR+9β2I2cp×2R=3I2cpR+24β2I2cpR(8)
K3=ΔP3ΔP=3I2cpR+24β2I2cpR3I2cpR=1+8β2(9)
比较式(5)、(7)、(9),显然,当负荷不平衡度β相等时,K3>K2>K1>1,对于三相四线制结线方式,由此可得出如下结论:
(1)三相四线制结线方式,当三相负荷平衡时线损最小;当一相负荷重,两相负荷轻的情况下线损增量较小;当一相负荷重,一相负荷轻,而第三相的负荷为平均负荷的情况下线损增量较大;当一相负荷轻,两相负荷重的情况下线损增量最大。
(2)当三相负荷不平衡时,不论何种负荷分配情况,电流不平衡度越大,线损增量也越大。
按照规程规定,不平衡度β不得大于20%。若使β=0.2,则K1=1.08,K2=1.11,K3=1.32,也就是说,相对于三相平衡的情况而言,由于三相负荷不平衡(且在规程允许范围内)所引起的线损分别增加8%、11%、32%。
下面绘出了负荷电流不平衡度β与功率损耗增量系数K的关系曲线。从曲线上可以明显地看出β对线损的影响。当然,上述各式和图2的关系曲线是在中性线的截面积为相线的一半时才成立,否则倍数值将改变,但只要β≠0,则K>1,上述两点结论依然成立。
为此在三相四线制的低压网络运行中,应经常测量三相负荷并进行调整,使之平衡,这是降损节能的一项有效措施,对于输送距离比较远的农村配电线路来说,效果尤为显著。