1. 半加器
仅由两数据相应位相加,不计进位的加法。若相应位为![]() ,相加后产生半加和和向高位进位
,相加后产生半加和和向高位进位![]() 。
。
真值表为:
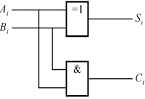 1)异或门、与门实现
1)异或门、与门实现
输出函数式为:![]() 。
。
2)全部“与非”门和全部“或非”门实现,必须把表达式变换成“与非-与非”式。
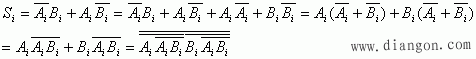
![]()
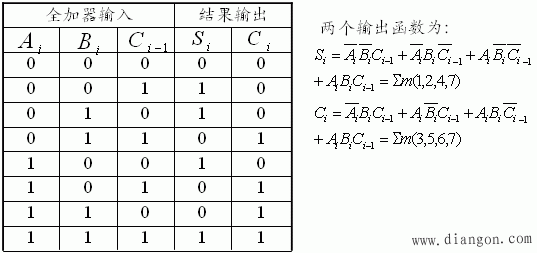
 实际上Si中的
实际上Si中的![]() 项是提取公共项得到的,这可用卡诺图来说明:
项是提取公共项得到的,这可用卡诺图来说明:
在二次结合时把![]() 格当作“1”了,然而总式中扣除该项即可。
格当作“1”了,然而总式中扣除该项即可。
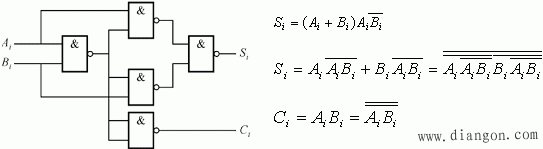
 3)全部用“或非”门实现,必须把表达式变换成“或非-或非”表达式。卡诺图中包围“0”格得“或与”表达式后,由二次求反得到:
3)全部用“或非”门实现,必须把表达式变换成“或非-或非”表达式。卡诺图中包围“0”格得“或与”表达式后,由二次求反得到:
![]() ,
,![]()
全部“或非”门实现的逻辑电路:
半加器的电路符号:![]()
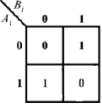
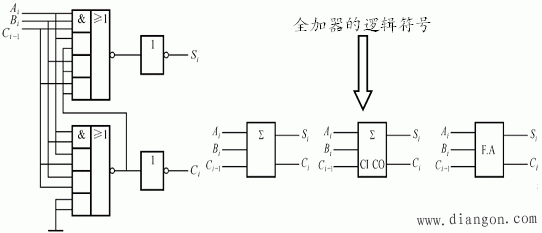
2. 全加器
能实现二个加数的对应位和相邻低位的进位一起相加的加法电路。令![]() ,
,![]() 为二数的相应位和低位进位,
为二数的相应位和低位进位,![]() 为全加后的和以及向高位的进位,则有真值表:
为全加后的和以及向高位的进位,则有真值表:
1)电路用“与非”门实现(略)。
2)用二个半加器实现。 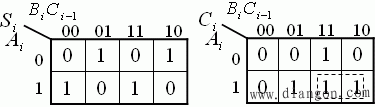
![]() ,
,![]()
二个半加器和“或”门实现: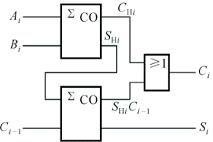
3)“与或”非门实现:将式子变换成“与—或—非”型式。方法:求![]() 时,把
时,把![]() 作为输入变量;求
作为输入变量;求![]() 时,把
时,把![]() 作为输入变量得出表达式。
作为输入变量得出表达式。

![]() ,
,![]()
二、多位二进制加法器
多位二进制加法电路种类很多,如四位并行输入串行进位加法电路,如图所示: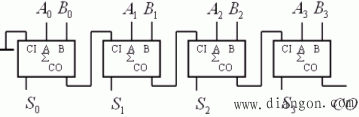
这种加法运算的速度是比较低的,在最不利的情况下,每做一次加法运算,需要经过4个全加器的传输延迟时间,才能得到稳定可靠的运算结果。
三、中规模集成超前进位加法器
为提高运算速度,必须设法减小或消除由于进位信号逐级传递所消耗的时间。那么高的进位输入信号能否在相加运算开始时就知道呢?因为第i位的进位输入信号![]() 是两个加数中第i-1位以下各位数据的函数,即有:
是两个加数中第i-1位以下各位数据的函数,即有:
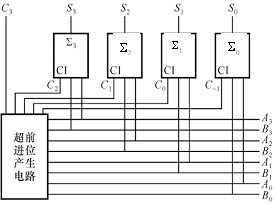
![]() ,因此,各超前进位输出信号的产生,可按图示方案实现:由一位全加器可知:
,因此,各超前进位输出信号的产生,可按图示方案实现:由一位全加器可知:
![]() ,
,![]()
其进位信号为:![]() 。
。
由此可得C-1,C0,C1,C2,C3 5个进位信号的逻辑函数。

![]()
四个全加和为:![]() ,
,![]()
![]() ,
,![]()
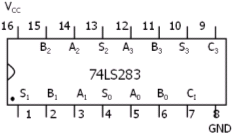
74LS283芯片就是按此方法设计的一个四位超前进位加法器电路: