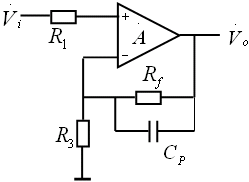
自激是指：电路没有输入信号，也会有输出。
下面电路是一个电压串联负反馈，假若电路具有三个极点频率，其频率特性表达式和开环对数幅频特性如下：
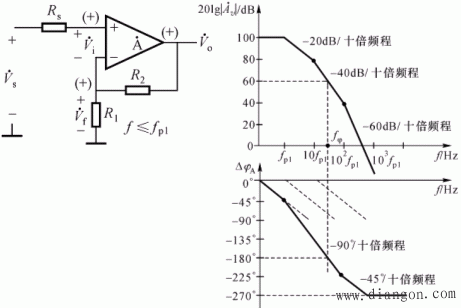
开环幅频特性表达式：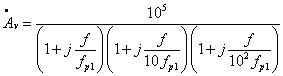
从频率特性曲线可知，在通频带以内，即
其附加相移还是小于
，所以引入的还是负反馈。 而在通频带以外，如在(fp)频率上，其此时的附加相移已是-
了(即
)，这说明，放大器在通频带以内是负反馈，但是在通频带以外的某一频率上，原负反馈已变成了正反馈了，这导致放大器工作不稳定，可能自激。由增益函数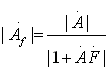
可知，当
时，闭环增益变为无穷大，即此时，无输入也会有输出，电路产生了自激。所以，产生自激的幅度条件为：。
也可写成：
(或20
)，(幅度平衡条件)；
，(相位平衡条件)。
负反馈放大器要产生自激振荡必须满足两个条件，幅度条件和相位条件。
在通频带以内，该电路是负反馈，而当在通频带以外，在波特图中的
其附加相移-，如果此时的信号
，该信号正好代替了
，即使为0，反馈回来的信号又经放大和反馈，如此不断的循环，电路会具有一定的输出。实际上，整个起振过程为：刚开始时环路增益
使反馈回来的信号不断加强，由于器件的非线性，
逐渐接近并等于1，振荡幅度达到平衡。
二、稳定判据和稳定裕度
一个负反馈放大器工作是否稳定，会不会产生自激振荡？可以通过产生自激的两个条件决定。
1. 稳定判据
方法：用环路增益的波特图来判断。
判据：(或20)，(幅度平衡条件)；
，(相位平衡条件)。
具体操作：①作出环路增益波特图；
② 从相位条件看幅度
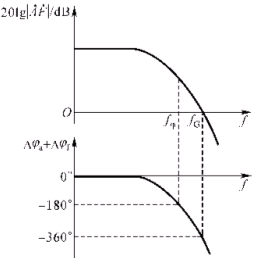
从波特图的
处，找幅频特性上的幅度
是＞0dB还是＜0dB，如＞0dB则一定自激；如＜0dB则放大电路工作稳定，不会自激。
③ 从幅度条件看相位
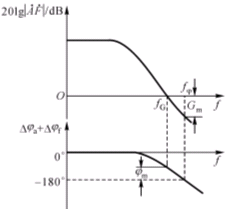
从=0dB处，找相频特性上的附加相移
，＞时，必定存在某一频率，满足幅度和相位条件，使放大器产生自激振荡；如果＜时，则不满足相位条件，放大电路工作稳定，不会产生自激。
2. 稳定裕度
为保证负反馈放大器在各种环境下都处于稳定的工作，工程上在
处的回路增益或在
处的相位都有一定的余量—裕度。它是衡量一个放大器工作是否稳定的重要指标。
裕度有两种标准：① 增益裕度Gm表示环路增益的附加相移
时，其对应的环路增益，即为增益裕度Gm(幅度裕度)，如图所示：
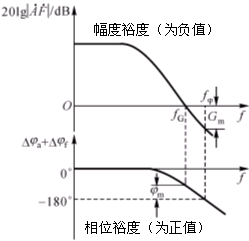
② 相位裕度
表示环路增益
处时，其对应的环路附加相移为相位裕度。 放大器的幅度裕度和相位裕度总称放大器的稳定裕度。
三、消除自激振荡的方法
思路：用相位补偿来破坏产生自激振荡的两个条件；
具体方法：在放大电路的适当地方加阻容元件(RC元件)，使环路增益的频率性发生变化，从而相位和幅度不满足自激条件。
1. 电容滞后补偿法
将补偿电容连接在前一级的输出电阻和后一级的输入电阻都比较大的回路，如下二个电路所示。它的目的是使决定上限的截止频率下移。
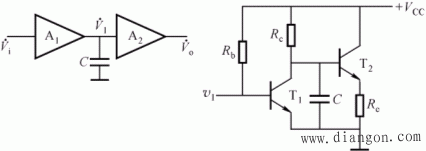
该两个电路的等效电路可以画成下面的形式：
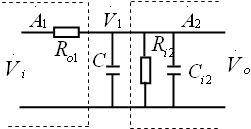
在未接补偿电容C前，其上限频率为：
接入补偿电容C后，上限频率变为：
现以三级开环幅频特性为例，补偿前的频率特性复数表达式为：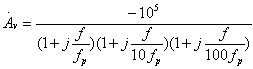
补偿后fp被fp’代替，所以表达式变为：
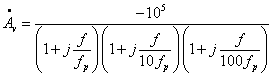
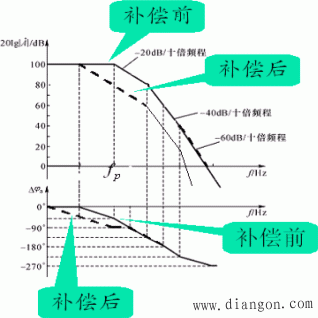
假定原
，补偿后
，则补偿后的频率特性如粗线所示。
补偿前后，同样以的相位裕度下：补偿前，反馈系数最大只可
，补偿后F可以为
，即可加深负反馈了。
该补偿优缺点：简单，方便；但上限频率下降了，通带变窄了。
2. 阻容滞后补偿法(RC滞后补偿)
该补偿也称零点—极点补偿，在原单接电容补偿的地方改接电阻R和电容C串联。它同样可以与电容补偿一样写出补偿前后的频率特性表达式，然后画出补偿前后的Bode Map，求出补偿后的上限频率和通带宽度。这种补偿同样使通带变窄，但比单纯用电容补偿时的通带要宽一些 。所以，普遍采用。
3. 密勒效应补偿法
补偿原理与前相同，只是此时可以用较小的电容值，就可起到明显补偿效果。这种补偿的电路如图所示：
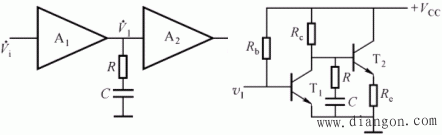
几种密勒效应补偿电路：
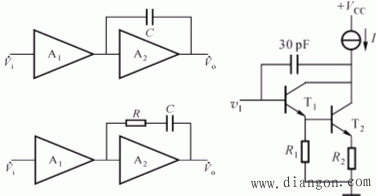
4. 相位超前补偿法
该种补偿的基本思路：设法在环路增益处的相位超前，使之不满足自激条件。这种补偿可以不损失通频带的宽度，但对电路参数苛刻，且较难调节。
