(1)测周期确定频率
可用测周期的方法,先测得信号的周期,再由信号的频率与周期是倒数关系,求倒数得到信号的频率。这种测量方法虽然精度不太高,但很方便,常用作频率的粗略测量。
(2)Lissajous图形法
1)被测频率fy的电压加到Y轴通道上,而把标准频率fx的电压加到X轴通道上,荧光屏上显示的图形称为Lissajous图形。
2)Lissajous图形的形状与输入的两个正弦信号的频率和相位差有关,因此可以通过对图形的分析来确定信号的频率及相位差(Lissajous图形法测相位差)。
Lissajous图形,如图1所示:
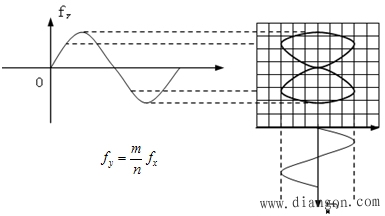
图1 Lissajous图形
确定m、n的数值:Lissajous图形应与X轴有2m个交点,与Y轴有2n个交点,所以只要从显示的Lissajous图形上数出这些交点,就可确定m、n的数值。
在Lissajous图形上分别作两条不通过图形本身的交点,也不与图形相切的水平线和垂直线,数出图形与水平线的交点即为2m,与垂直线的交点为2n。
Lissajous图形法一般适用于被测频率和标准频率十分稳定的低频信号(音频到几兆赫范围),而且一般要求两频率比最大不超过10倍,否则图形过于复杂而难以测准。
如果fy与fx不成比例关系,则荧光屏上显示的图形是不稳定的或旋转变化的,这时还应该继续调节标准频率信号源,直到图形稳定。只有当fy:fx=m:n(m,n为整数)时,荧光屏上才能显示稳定的图形。由于标准信号源的频率是已知的,只要能确定比值m:n,就可算出被测信号频率。
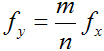
不同频率比和不同相位差的Lissajous图形,如图2所示:
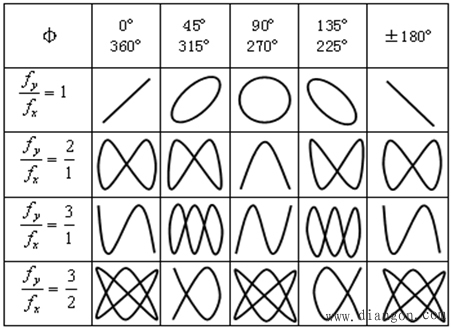
图2 不同频率比和不同相位差的Lissajous图形
2、计数法测量频率
(1)原理
计数法测量频率,如图3所示:
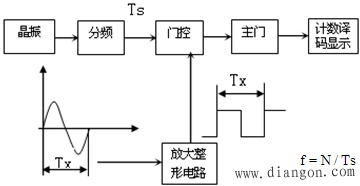
图3 计数法测量频率
(2)量化误差(±1误差)
1)产生原因
在计数时,如果主门的开启信号与被测信号之间没有同步锁定关系,同一被测信号在相同的主门开启时间内两次测量所记录的脉冲数N可能不一样。
±1误差示义图,如图4所示:
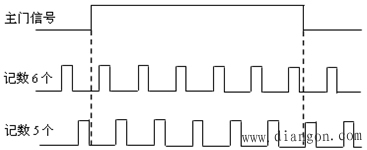
图4 ±1误差示义图
2)量化误差
量值最大计算误差ΔN=±1,它称为量化误差或±1误差。最大计数相对误差的形式为
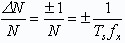
当主门控制信号Ts的误差不能忽略,总误差可采用分项误差绝对值合成得到
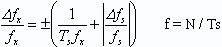
式中:Δfs/fs——标准频率误差,是晶振频率的准确度
3、拍频法
(1)拍频法
是将被测频率与标准频率相比较。被测频率fX的信号与标准频率fS的信号同时加到一个线性元件——耳机上。
(2)如果改变频率fS使之非常接近频率fX时(例如两频率之间相差5Hz左右),就分不出两个信号频率(音调)上的差别了,此时视为零拍。这时只听到一介于两个音调之间的音调,同时,声音的响度(振幅)随时间作周期性变化。这种现象在声学上称为拍。声音的响度变化频率正好就是两频率之差|fX-fS|。当两频率完全相等时,合成波的幅度就不变化了。
拍频法测量音频的方框图,如图5所示:
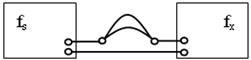
图5 拍频法测量音频的方框图
(3)数学推导
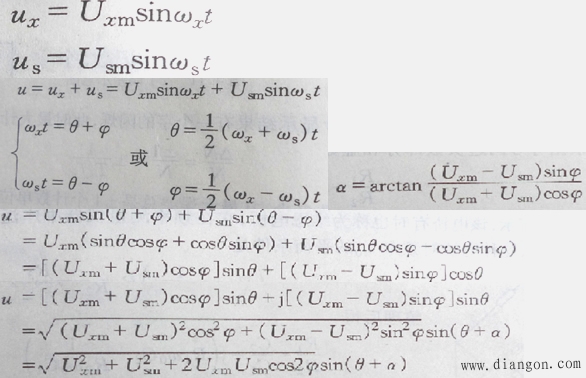

4、电桥法
(1)电桥法只用来测量音频频率。(高频时寄生电感和电容对电桥的调节有很大的影响)
(2)根据电路原理的知识,我们知道,如果把一电压加到电桥的一个对角线上,通过调节对应的元件就可以使电桥的另一对角线上的电压为零,即电桥达到了平衡。如果电桥平衡的条件(桥臂上存在电感和电容元件)与所加电压的频率有关,则该电桥就可以用于测量频率。常用的电桥法有谐振电桥、电容电桥和双T电桥。
1)谐振电桥
首先,适当选取可变电阻R1的值,然后调节电感和电容使回路对所加电压的频率谐振,这样回路的阻抗才是纯电阻,才能测出被测频率。该方法缺点是改变被测频率Fx时,每次不仅要把回路调节到谐振,同时还要调节电阻R1,并且测量低频时回路较笨重。
谐振电桥电路,如图6所示:
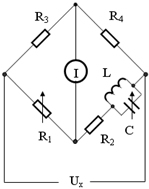
图6 谐振电桥电路
2)电容电桥
A、可以用电阻或电容来改变电桥的频率。
B、在被测频率的电压中有谐波时,就很难使电桥达到平衡。因为,电桥对基波平衡了,对谐波则不平衡。这种电桥仅适用于10KHz以下的音频范围。
电容电桥电路,如图7所示:
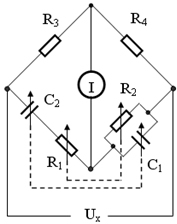
图7 电容电桥电路
C 、数学推导
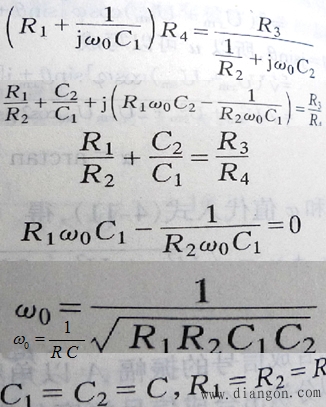
3)双T电桥
被测频率的信号源与指示器具有共同的接地点通过改变电阻R1和R2,来平滑调节频率。测量频率的误差一般为0.5~1%。
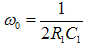
双T电桥电路,如图8所示:
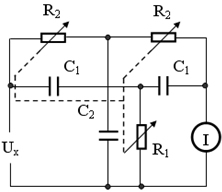
图8双T电桥电路
