电力系统稳定

电力系统稳定问题
——当系统在某一正常运行状态下受到某种干扰后，能否经过一段时间后回到原来的运行状态或者过渡到一个新的稳态运行状态的问题。
根据扰动的大小，电力系统稳定问题可分为：
电力系统的静态稳定性
对于隐极发电机与无限大功率系统相连的情况，可以作出相量图和发电机功-角特性方程：


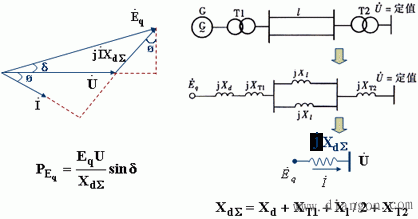
设发电机原动机的机械功率为P_m，且不可调，忽略摩擦等损耗，则在发电机功-角特性曲线上将有两个运行点：a和b。
a是静态稳定运行点。


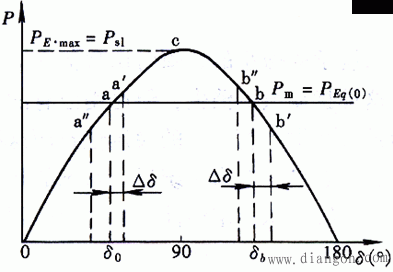
静态稳定的储备
可见，功率角δ=90°时对应的c点是静态稳定运行的临界点，这时对应的功率是系统传输的最大功率，称为静态稳定极限，以P_sl表示。
实际电力系统是不可能在静态稳定极限状态运行的。为了说明系统运行情况是否接近静态稳定极限，常用静态稳定储备系数K_p来衡量：



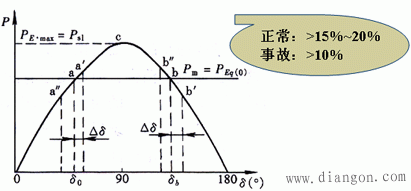
保证和提高静态稳定的措施
根本措施：缩短“电气距离”。

1）采用自动调节励磁装置
某些发电机自动调节励磁装置可使E_q’=常数，所呈现的电抗为暂态电抗X_d’。
2）减少线路电抗
采用分裂导线。
3）提高线路额定电压
4）采用串联电容器补偿
5）改善电力系统结构
分析暂态稳定时的功-角特性
如果发电机用X’_d和E’表示的近似数学模型(δ’以δ表示），则可以推导出正常运行时的功-角特性方程为：

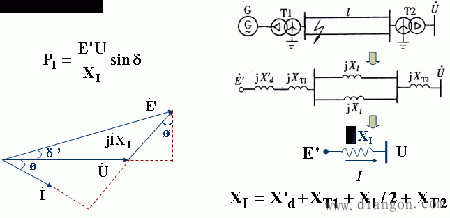
在发生短路故障时，相当于在短路点接入一个附加电抗 :

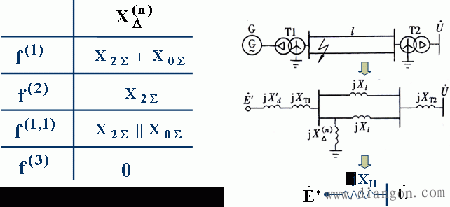
这时的功-角特性方程为：


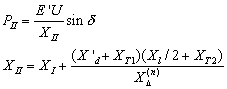
在短路故障线路被切除后，功-角特性方程为：


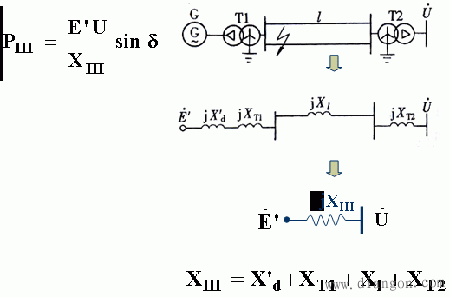
通常X_I<X_III<X_II，所以曲线P_III介于P_I和P_II之间。
正常运行：a点。

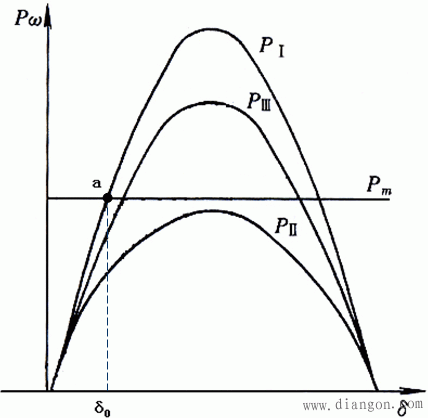
等面积定则
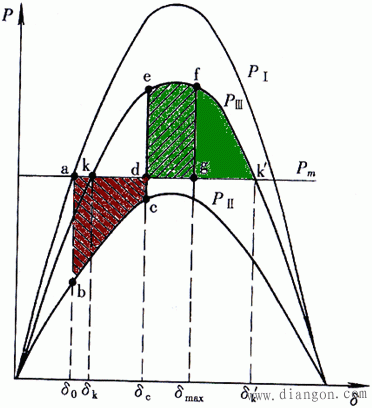
在功角δ₀变化到δ_c的过程中，原动机输入的机械功率P_m >发电机输出的电磁功率P_e ，转子加速，过剩的能量转变成转子的动能而储存到转子中。过剩转矩所作的功为：

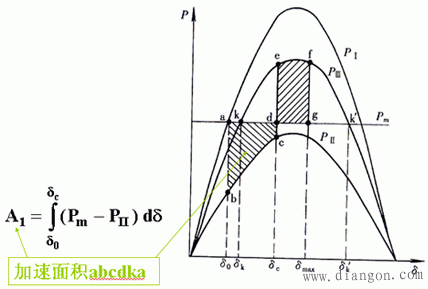
在功角δ_c变化到δ_max的过程中，原动机输入的机械功率P_m <发电机输出的电磁功率P_e ，转子减速，将转子中储存的动能转变成电磁能。所消耗的动能为：


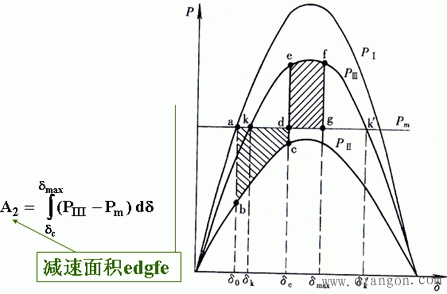
当功角达到δ_max时，转子重新达到同步转速（ω=ω_N），说明在加速期间积蓄的动能增量全部耗尽，即加速面积和减速面积大小相等，这就是等面积定则：



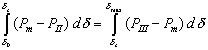
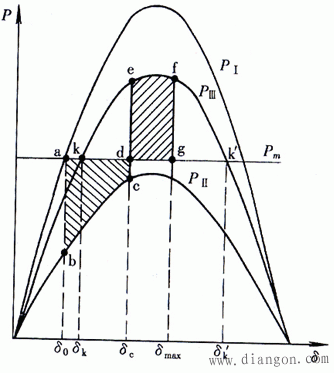
根据等面积定则，系统暂态稳定的条件是最大减速面积edgk’fe大于加速面积abcdka，即：



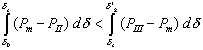
极限切除角δ_c.cr——系统保持暂态稳定的前提下所允许的最大切除角。
由下式可求得极限切除角：


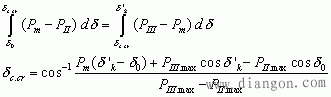
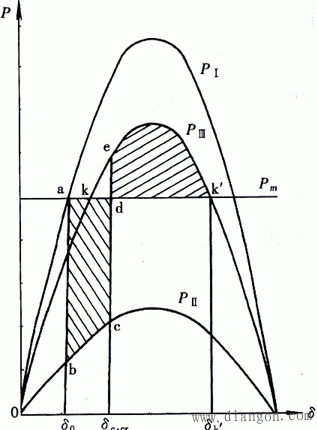
提高暂态稳定的措施
优先措施：考虑减少功率或能量的差额。
1）快速切除故障和自动重合闸
2）强行励磁和快速关闭汽门
3）电气制动和变压器中性点经小电阻接地
4）采用单元接线
5）连锁切机和切除部分负荷
6）系统解列