加工直线时两轴的输入指令为:

由于存在跟随误差△DX 、 △DY在某时刻指令位
置在A点,实际位置在A′点,则有:
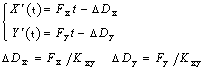

轮廓误差ε的几何求法:

式中:KS:平均系统增益
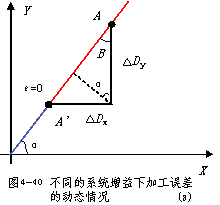
跟随误差△DX 、△DY对轮廓精度无影响。如图4-40a所示。
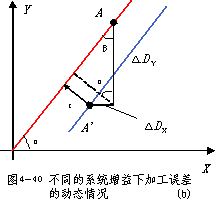

![]() 当两轴增益不一致,但KSX 、KSY
当两轴增益不一致,但KSX 、KSY
常数时,KS、△KS 为常数,则ε为常数,
也就是说,直线的轮廓形状无误差,但位
置偏离了原位置。
如图4-40b所示。
![]() 当两轴增益不一致,KSX 、KSY
当两轴增益不一致,KSX 、KSY
也不是常数时,则ε不是常数,也就是说,
将产生轮廓形状误差,即加工出的轮廓就
不是直线了。如图4-40c所示。
![]() 在其它条件不变的情况下:
在其它条件不变的情况下:
① 轮廓误差ε与△KS 成正比,
与KS的平方成反比与进给速度成F正比。
② 当加工45°直线时,轮廓误差ε最大。
③ 当加工0°或90°直线时,轮廓误差ε
与增益无关。
![]() 例题
例题
在 X-Y 平面上铣削工件的一个平面, 该面与 X 轴成45°角,
进给速度为:F = 450 mm/min,KS为15±2% (1/s),计算最大轮廓误差εmax。
解:
 2.跟随误差对圆弧轮廓加工精度的影响
2.跟随误差对圆弧轮廓加工精度的影响
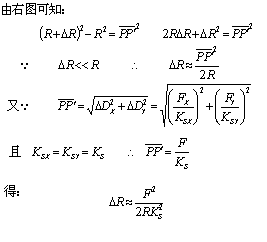
△D对园弧轮廓加工精度的影响可用加工圆弧的半径变动量△R描述。 通常△R 的变化较为复杂,为此,可先讨论下面条件下的情况:
KSX = KSY = KS
然后再定性的讨论其它较为复杂的情况。
![]() △R 的求取(如图4-41)
△R 的求取(如图4-41)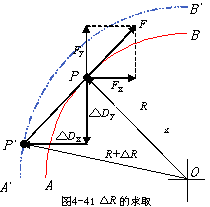
![]() 讨论
讨论
![]() 当KSX = KSY,且进给速度F为恒速时,△R是常数。只产生尺寸误差,不产生形状
当KSX = KSY,且进给速度F为恒速时,△R是常数。只产生尺寸误差,不产生形状
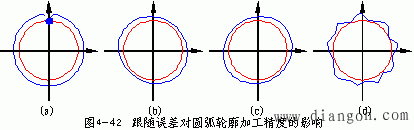
误差。当从圆上某一点开始加工整圆时,则实际轨迹如图4-42a所示,为什么?请学员思考。
![]() 当KSX≠KSY时,此时不仅产生尺寸误差,而且产生形状误差。可以证明:
当KSX≠KSY时,此时不仅产生尺寸误差,而且产生形状误差。可以证明:
① 当KSX=aKSY(a为常数)时,圆弧插补所形成的形状为椭圆(长轴与X轴成45°夹角)。
则实际轨迹如图4-42b、c所示;
② 当KSX与KSY无确定关系时,圆弧插补所形成的形状为无规则的形状。则实际轨迹
如图4-42d所示。
![]() 在条件一定的情况下:
在条件一定的情况下:
① 轮廓误差△R 与 KS 的平方成反比;轮廓误差△R与 F 的平方成正比。因此,
KS↑或 F↓ 可大大提高轮廓加工精度。
② 轮廓误差△R与加工园弧的半径R 成反比。在小圆弧加工时,要保证加工精度,
进给速度F不能太高。
综上所述,在数控系统中,各轴进给伺服系统的增益均稍有差别,在进行轮廓加工时会产生轮廓误差,因此,要求各轴的KS 值尽量接近,尤其是在低增益系统。目前先进的CNC系统均带有跟随误差△D的监视和 KS 值的显示功能。
