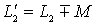含有耦合电感电路的计算

含有耦合电感（简称互感）电路的计算要注意：
　　(1) 在正弦稳态情况下，有互感的电路的计算仍可应用前面介绍的相量分析方法。
　　(2) 注意互感线圈上的电压除自感电压外，还应包含互感电压。

(3) 一般采用支路法和回路法计算。因为耦合电感支路的电压不仅与本支路电流有关，还与其他某些支路电流有关，若列结点电压方程会遇到困难，要另行处理。 　 1. 耦合电感的串联 　　（1） 顺向串联
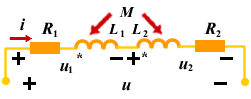	图 1

　　图1所示电路为耦合电感的串联电路，由于互感起“增助”作用，称为顺向串联。

按图示电压、电流的参考方向，KVL方程为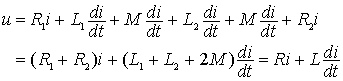： 　　　 　根据上述方程可以给出图2所示的无互感等效电路。等效电路的参数为：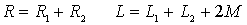
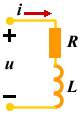	图 2

（2） 反向串联 　　图3 所示的耦合电感的串联电路，由于互感起“削弱”作用，称为反向串联。 　　按图示电压、电流的参考方向，KVL方程为：
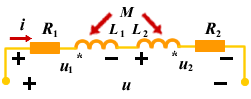	图 3

　　　　　　
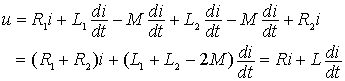
　　根据上述方程也可以给出图2所示的无互感（去耦）等效电路。但等效电路的参数为：
　　　　　　　
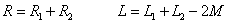
　　在正弦稳态激励下，应用相量分析，图1和图3的相量模型如图4所示。

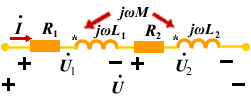图4 （a）	图 4（b）

图（a）的 KVL 方程为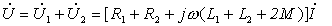： 　 　　输入阻抗为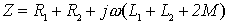： 　　 　　可以看出耦合电感顺向串联时，等效阻抗大于无互感时的阻抗。顺向串联时的相量图如图5 所示。 　　图（b）的 KVL 方程为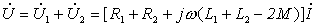： 　 　输入阻抗为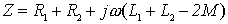： 　　可以看出耦合电感反向串联时，等效阻抗小于无互感时的阻抗。反向串联时的相量图如图 6所示。
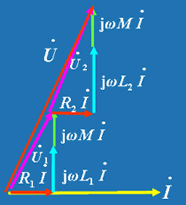	图 5

注意： 　　（1） 互感不大于两个自感的算术平均值，整个电路仍呈感性，即满足关系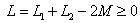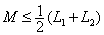： 　　　　 　　（2）根据上述讨论可以给出测量互感系数的方法：把两线圈顺接一次，反接一次，则互感系数为：
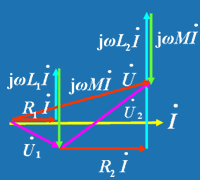	图 6

　　2. 耦合电感的并联　
　　 （1）同侧并联
　　图 7为耦合电感的并联电路，由于同名端连接在同一个结点上，称为同侧串联。

根据 KVL 得同侧并联电路的方程为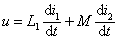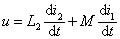： 　　　　　 　　由于 i = i1 + i2 　　　解得 u , i 的关系：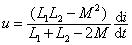
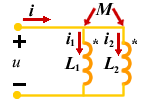	图 7

根据上述方程可以给出图8 所示的无互感等效电路，其等效电感为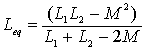： 　　　　　　　 　 （2） 异侧并联
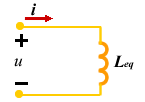	图 8

　　图 9中由于耦合电感的异名端连接在同一个结点上，故称为异侧并联。

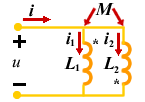	此时电路的方程为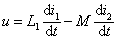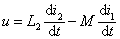： 　　 考虑到： i = i1 + i2 　　 解得 u , i 的关系：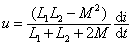
图 9

　　根据上述方程也可以给出图9 所示的无互感等效电路，其等效电感为：
　　　　　　　
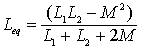
　　3. 耦合电感的 T 型去耦等效

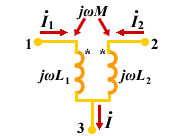
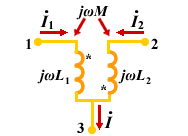
如果耦合电感的2 条支路各有一端与第三条支路形成一个仅含三条支路的共同结点如图 10所示，称为耦合电感的 T 型联接。显然耦合电感的并联也属于 T 型联接。
	图 10	图 11

　　（1）同名端为共端的T 型去耦等效
　　图10的电路为同名端为共端的 T 型联接。根据所标电压、电流的参考方向得：
　　　　　　 　　
　　　　　　
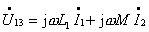
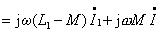
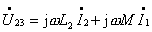
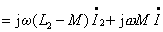
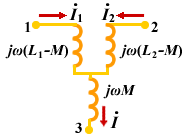
　　由上述方程可得图11所示的无互感等效电路。
　　（2） 异名端为共端的 T 型去耦等效

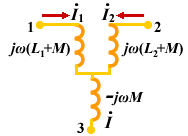图 12	图 13

　　　　图 12的电路为异名端为共端的 T 型联接。根据所标电压、电流的参考方向得：
　　　　
　　　　
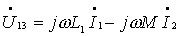
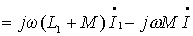
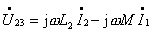
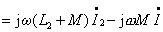
　　由上述方程可得图13所示的无互感等效电路。
　　注意： T 型去耦等效电路中 3 条支路的等效电感分别为：
　　　支路 3 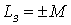： （同侧取“ + ”，异侧取“—”）
　　　支路 1 ：
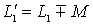
　　　支路 2 ：