周期函数分解为付里叶级数

电工技术中所遇到的非正弦周期电流、电压信号多能满足展开成傅里叶级数的条件，因而能分解成如下傅里叶级数形式：
　　　　
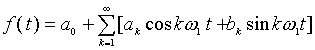
　　　也可表示成：
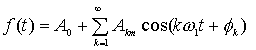
　　以上两种表示式中系数之间关系为：
　　　　　　
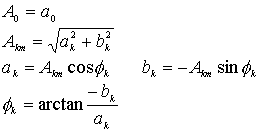
　　上述系数可按下列公式计算：
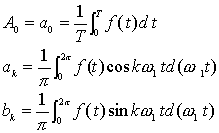　　　　　　 　　　（k=1，2，3……）

求出a0、ak、bk 便可得到原函数 f(t) 的展开式。 　 注意： 非正弦周期电流、电压信号分解成傅里叶级数的关键在于求出系数a0、ak、bk ，可以利用函数的某种对称性判断它包含哪些谐波分量及不包含哪些谐波分量，可使系数的确定简化，给计算和分析将带来很大的方便。如以下几种周期函数值得注意： (1) 偶函数 　波形对称与纵轴如图 2 所示， 　　满足： (2) 奇函数 　波形对称与原点如图 3 所示， 　　满足： (3) 奇谐波函数 　波形镜对称如图 4 所示，满足： (4) 若函数是偶函数又是镜对称时，则只含有奇次的余弦相，即 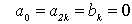(5) 若函数是奇函数又是镜对称时，则只含有奇次的正弦相，即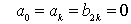
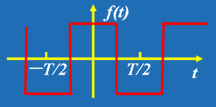	图 2
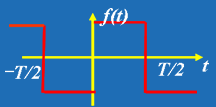	图 3
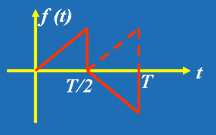	图 4

　　实际中所遇到的周期函数可能较复杂，不易看出对称性，但是如果将波形作一定的平移，或视为几个典型波形的合成，则也能使计算各次谐波的系数简化。